Spis rzeczy

Przestrzenie unitarne, iloczyn skalarny

Niech dana będzie przestrzeń liniowa $X$. Załóżmy, że każdej parze elementów $x,y\in X$ została przyporządkowana liczba $\left( x,y\right) \in\mathbb{C}$ (lub $\mathbb{R}$), przy czym przyporządkowanie to spełnia warunki:

$1^{\circ}$

$\left( x,y\right) =\overline{\left( y,x\right) }$,

$2^{\circ}$

$\left( x+y,z\right) =\left( x,z\right) +\left(y,z\right)$,

$3^{\circ}$

$\left( \alpha x,y\right) =\alpha\left( x,y\right)$,

$4^{\circ}$

$\left( x,x\right) >0$ dla $x\neq0$, $\left( 0,0\right)=0$.

Liczbę $\left( x,y\right)$ nazywamy iloczynem skalarnym elementów $x$, $y$.

Warunki $1^{\circ}-4^{\circ}$ są aksjomatami iloczynu skalarnego.

U w a g a

Prawdziwe są także wzory:

a)

$\left( z,x+y\right) =\left( z,x\right) +\left( z,y\right)$,

b)

$\left( x,\alpha y\right) =\overline{\alpha}\left( x,y\right)$.

Wynikają one bezpośrednio z aksjomatów iloczynu skalarnego.
 

T w i e r d z e n i e (tzw. nierówność Schwarza)

Iloczyn skalarny spełnia nierówność

$$\left\vert \left( x,y\right) \right\vert ^{2}\leq\left( x,x\right) \left( y,y\right)$$ (10.1)

Dla dowodu wystarczy zauważyć, że dla dowolnego $t\in\mathbb{R}$ i dowolnego elementu $y\neq0$ zachodzi nierówność $\left(x+ty,x+ty\right) \geq0$. Z aksjomatów iloczynu skalarnego wynika, że

$$\left( x+ty,x+ty\right) =\left( x,x\right) +\overline{t}\left(x,......verline{\left( x,y\right) }+\left\vert t\right\vert ^{2}\left(y,y\right) \geq0$$. Podstawiając $$t=-\frac{\left( x,y\right) }{\left( y,y\right) }%%$$ do powyższej nierówności otrzymujemy ostatecznie $$\left( x,x\right) -\frac{\left\vert \left( x,y\right) \right\vert ^{2}}{\left(y,y\right) }\geq0$$ co jest równoważne nierówności (10.1), a zatem kończy dowód.
 

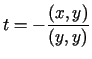
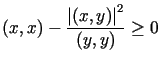
U w a g a   1

Można pokazać, że nierówność Schwarza (10.1) staje się równością wtedy i tylko wtedy, gdy elementy $x$ i $y$ są liniowo zależne.

U w a g a   2

Jeżeli $\left( x,y\right)$ jest iloczynem skalarnym w przestrzeni liniowej $X$, to wzór

$$\Vert x\Vert=\sqrt{\left( x,x\right) }%%$$ (10.2)

określa normę w przestrzeni $X$.

Z definicji normy, aksjomatów iloczynu skalarnego i nierówności Schwarza wynika, że

$$\Vert x+y\Vert^{2} =\left( x+y,x+y\right) =\left( x,x\right) +\left( x,y\right) +\left( y,x\right) +\left( y,y\right) \leq$$

$$\leq\left( x,x\right) +2\left\vert \left( x,y\right) \right\vert ......right) +2\sqrt{\left( x,x\right) }\sqrt{\left( y,y\right) }+\left( y,y\right) =$$

$$=\Vert x\Vert^{2}+2\Vert x\Vert\Vert y\Vert+\Vert y\Vert^{2}=\left( \Vert x\Vert+\Vert y\Vert\right) ^{2}$$

oraz

$$\Vert\alpha x\Vert=\sqrt{\left( \alpha x,\alpha x\right) }=\sqrt......\overline{\alpha}\left( x,x\right) }=\left\vert \alpha\right\vert \Vertx\Vert$$ co kończy dowód.
 

D e f i n i c j a

Zbiór $X$ nazywamy przestrzenią unitarną, jeżeli:

$1^{\circ}$

$X$ jest przestrzenią liniową,

$2^{\circ}$

w $X$ określony jest iloczyn skalarny $\left( x,y\right)$,

$3^{\circ}$

w $X$ zdefiniowana jest norma wzorem (10.2).

D e f i n i c j a

$X$ jest przestrzenią Hilberta wtedy i tylko wtedy, gdy$X$ jest przestrzenią unitarną zupełną (zupełność oznacza, że każdy ciąg spełniający warunek Cauchy'ego zbieżności ciągu ma granicę należącą do tej przestrzeni).