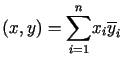Spis rzeczy

Subsections

• Przestrzeń euklidesowa n-wymiarowa rzeczywista lub zespolona
• Przestrzeń ciągów sumowalnych z kwadratem
• Przestrzeń funkcji całkowalnych z kwadratem

Przykłady przestrzeni Hilberta

Przestrzeń euklidesowa n-wymiarowa rzeczywista lub zespolona

Niech $X=\mathbb{R}^{n}$ lub $X=\mathbb{C}^{n}$ i niech $x=\left( x_{1}%%,x_{2},\ldots,x_{n}\right)$, $y=\left( y_{1},y_{2},\ldots,y_{n}\right) \inX$.

Iloczyn skalarny definiujemy jako

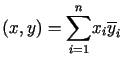$$\left( x,y\right) =<tex2html_comment_mark>1648 {\displaystyle\sum\limits_{i=1}^{n}} x_{i}\overline{y}_{i}$$ (10.3)

Wtedy

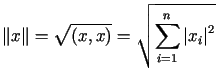$$\Vert x\Vert=\sqrt{\left( x,x\right) }=\sqrt{<tex2html_comment_mark>1653 {\displaystyle\sum\limits_{i=1}^{n}} \left\vert x_{i}\right\vert ^{2}}$$ (10.4)

Nierówność Schwarza (10.1) przybiera równoważną postać

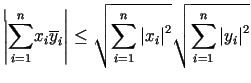$$\left\vert {\displaystyle\sum\limits_{i=1}^{n}} x_{i}\overline{y}......>1665 {\displaystyle\sum\limits_{i=1}^{n}} \left\vert y_{i}\right\vert ^{2}}%%$$ (10.5)

i znana jest pod nazwą nierówności Cauchy'ego.

Zupełność przestrzeni $\mathbb{R}^{n}$ (lub $\mathbb{C}^{n}$) wynika z zupełności zbioru liczb rzeczywistych i zespolonych.

Przestrzeń ciągów sumowalnych z kwadratem

Niech $X=l^{2}$ będzie przestrzenią ciągów rzeczywistych lub zespolonych $\left( \xi_{k}\right)$ takich, że $$%%{\displaystyle\sum\limits_{k=1}^{+\infty}}\left\vert \xi_{k}\right\vert ^{2}<\infty,$$ ze zwykłymi działaniami dodawania ciągów po współrzędnych i mnożenia przez liczbę.

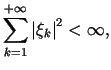
Iloczyn skalarny ciągów $x=\left( \xi_{k}\right)$ i $y=\left(\eta_{k}\right)$ definiujemy jako

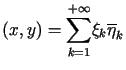$$\left( x,y\right) =<tex2html_comment_mark>1674 {\displaystyle\sum\limits_{k=1}^{+\infty}} \xi_{k}\overline{\eta}_{k}$$ (10.6)

Poprawność powyższej definicji wynika z oszacowania $\left\vert\xi_{k}\overline{\eta}_{k}\right\vert \leq\frac{1}{2}\left( \left\vert \xi_{k}\right\vert ^{2}+\left\vert \eta_{k}\right\vert ^{2}\right)$.

Z definicji normy wynika, że

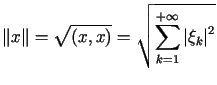$$\Vert x\Vert=\sqrt{\left( x,x\right) }=\sqrt{<tex2html_comment_ma...... {\displaystyle\sum\limits_{k=1}^{+\infty}} \left\vert \xi_{k}\right\vert ^{2}}$$ (10.7)

Nierówność Schwarza przybiera postać

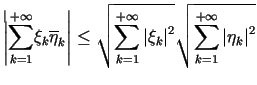$$\left\vert {\displaystyle\sum\limits_{k=1}^{+\infty}} \xi_{k}\ove......isplaystyle\sum\limits_{k=1}^{+\infty}} \left\vert \eta_{k}\right\vert ^{2}}%%$$ (10.8)

(jest to tzw. nierówność Cauchy'ego dla szeregów).

Dowodzi się, że przestrzeń $X=l^{2}$ jest zupełna.

Przestrzeń funkcji całkowalnych z kwadratem

Niech $X=L^{2}\left( \Omega\right)$ będzie przestrzenią funkcji$f\left( x\right)$ określonych na zbiorze $\Omega\subset\mathbb{R}^{n}$ o wartościach rzeczywistych lub zespolonych takich, że $$%%{\displaystyle\int\limits_{\Omega}}\left\vert f\left( x\right) \right\vert ^{2}dx<\infty$$. Zakładamy, że $\left\vert \Omega\right\vert >0$, gdzie $\left\vert \Omega\right\vert$ oznacza miarę zbioru $\Omega$. W przestrzeni $L^{2}\left(\Omega\right)$ wprowadzamy zwykłe działania dodawania funkcji i mnożenia funkcji przez liczby.

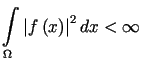Iloczyn skalarny definiujemy jako

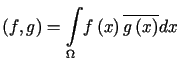$$\left( f,g\right) =<tex2html_comment_mark>1701 {\displaystyle\int\limits_{\Omega}} f\left( x\right) \overline{g\left( x\right) }dx$$ (10.9)

Jego istnienie wynika z nierówności $\left\vert f\left( x\right)\overline{g\left( x\right) }\right\vert \leq\frac{......x\right) \right\vert ^{2}+\left\vert g\left( x\right) \right\vert ^{2}\right)$.

Normę definiujemy następująco

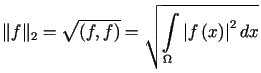$$\Vert f\Vert_{2}=\sqrt{\left( f,f\right) }=\sqrt{<tex2html_commen......splaystyle\int\limits_{\Omega}} \left\vert f\left( x\right) \right\vert ^{2}dx}$$ (10.10)

Nierówność Schwarza jest postaci

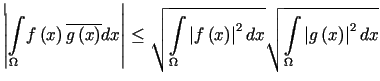$$\left\vert {\displaystyle\int\limits_{\Omega}} f\left( x\right) \......aystyle\int\limits_{\Omega}} \left\vert g\left( x\right) \right\vert ^{2}dx}%%$$ (10.11)

i znana jest pod nazwą nierówności Buniakowskiego dla całek.

Można dowieść, że przestrzeń $L^{2}\left(\Omega\right)$ jest zupełna.

Zbieżność w przestrzeni $L^{2}\left(\Omega\right)$ nie jest równoważna zbieżności punktowej, ale prawdziwe jest następujące twierdzenie.

T w i e r d z e n i e

Jeśli $f_{n}\rightarrow f_{0}$ w $L^{2}\left(\Omega\right)$ i$f_{n}\left( x\right) \rightarrow f\left( x\right)$ prawie wszędzie na $\Omega$, to $f\in L^{2}\left( \Omega\right)$ i $f=f_{0}$.