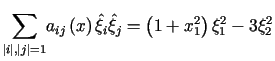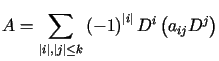 , , |
(12.1) |
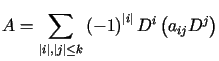 , , |
(12.1) |
gdzie ![]() oraz
oraz ![]() są wielowskaźnikami,
są wielowskaźnikami, ![]() .
.
P r z y k ł a d y (dla n=2)
| (12.2) |
Wtedy
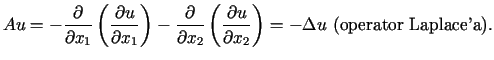
![$\displaystyle a_{ij}=\left\{ \begin{array}[c]{cl}<tex2html_comment_mark>1996 1 ......w pozosta\l ych przypadkach.}<tex2html_comment_mark>1997 \end{array} \right.%%$](img1620.gif) |
(12.3) |
Wtedy
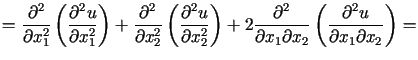 |
||
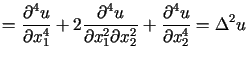 (operator biharmoniczny).
(operator biharmoniczny). |
U w a g a
Operator ![]() nie wyznacza jednoznacznie przedstawienia (12.1).
Dla każdego operatora można na ogół wybrać różne reprezentacje, w zależności
od prowadzonych rozważań. Np. operator Laplace'a może być otrzymany również
przez przyjęcie współczynników
nie wyznacza jednoznacznie przedstawienia (12.1).
Dla każdego operatora można na ogół wybrać różne reprezentacje, w zależności
od prowadzonych rozważań. Np. operator Laplace'a może być otrzymany również
przez przyjęcie współczynników ![]() jako
jako
![$\displaystyle a_{ij}=\left\{ \begin{array}[c]{rl}<tex2html_comment_mark>2003 1 ......}j=\left( 1,0\right) \text{.}<tex2html_comment_mark>2004 \end{array} \right.%%$](img1625.gif) |
(12.4) |
D e f i n i c j a
Mówimy, że operator ![]() określony równością (12.1) jest eliptyczny
w punkcie
określony równością (12.1) jest eliptyczny
w punkcie ![]() wtedy i tylko wtedy gdy dla każdego układu
wtedy i tylko wtedy gdy dla każdego układu ![]() zachodzi
zachodzi
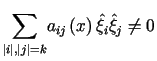 , , |
(12.5) |
gdzie ![]() ,
,![]() .
.
D e f i n i c j a
Mówimy, że operator ![]() określony równością (12.1) jest jednostajnie
eliptyczny w obszarze
określony równością (12.1) jest jednostajnie
eliptyczny w obszarze ![]() wtedy i tylko wtedy gdy istnieje liczba
wtedy i tylko wtedy gdy istnieje liczba ![]() zależna tylko od obszaru
zależna tylko od obszaru ![]() i wpółczynników
i wpółczynników ![]() taka, że dla prawie wszystkich punktów
taka, że dla prawie wszystkich punktów ![]() i dla wszystkich
i dla wszystkich ![]() zachodzi
zachodzi
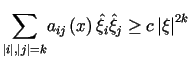 , , |
(12.6) |
gdzie ![]() .
.
P r z y k ł a d y
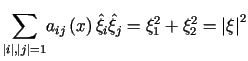 ,
,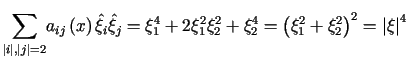 .
.![$\displaystyle Au=-\frac{\partial}{\partial x_{1}}\left[ \left( 1+x_{1}^{2}\righ......partial u}{\partial x_{1}}\right] +3\frac{\partial^{2}u}{\partialx_{2}^{2}}%%$](img1638.gif)