| (12.7) |
| (12.7) |
Niech ![]() ,
, ![]() ,
,![]() - będzie rozwiązaniem klasycznym tego równania. Niech ponadto
- będzie rozwiązaniem klasycznym tego równania. Niech ponadto![]() .
Wówczas
.
Wówczas
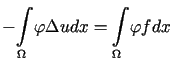 . . |
(12.8) |
Stosując do lewej strony powyższej równości twierdzenie Greena postaci
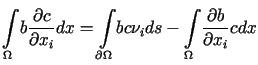 dla
dla 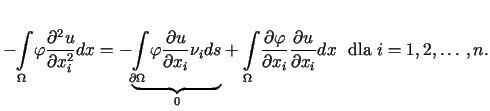
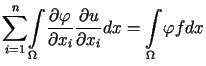 |
(12.9) |
dla dowolnej funkcji![]() .
.
Tożsamość (12.9) ma sens nawet wtedy,
gdy równanie (12.7) nie ma rozwiązań klasycznych
należących do![]() np. wtedy, gdy funkcja
np. wtedy, gdy funkcja ![]() i
i ![]() nie jest funkcją ciągłą. W tym przypadku uzasadnione jest przyjęcie następującej
definicji słabego (lub uogólnionego) rozwiązania rozważanego
równania różniczkowego.
nie jest funkcją ciągłą. W tym przypadku uzasadnione jest przyjęcie następującej
definicji słabego (lub uogólnionego) rozwiązania rozważanego
równania różniczkowego.
D e f i n i c j a
Niech ![]() ,
, ![]() .
Jeżeli dla każdej funkcji
.
Jeżeli dla każdej funkcji ![]() zachodzi tożsamość (12.9), to mówimy, że
zachodzi tożsamość (12.9), to mówimy, że ![]() jest słabym (uogólnionym) rozwiązaniem równania (12.7).
jest słabym (uogólnionym) rozwiązaniem równania (12.7).
Koncepcja słabego rozwiązania jest znacznie ogólniejsza od koncepcji
rozwiązania klasycznego, np. słabe rozwiązanie równania rzędu drugiego
może nie posiadać pochodnych (nawet w sensie dystrybucyjnym) rzędu drugiego.
Ponadto, jeżeli ![]() jest rozwiązaniem równania (12.7) w sensie
powyższej definicji oraz
jest rozwiązaniem równania (12.7) w sensie
powyższej definicji oraz![]() ,
, ![]() ,
to stosując ponownie wzór Greena łatwo pokazać, że
,
to stosując ponownie wzór Greena łatwo pokazać, że ![]() jest także rozwiązaniem w sensie klasycznym.
jest także rozwiązaniem w sensie klasycznym.
Analogiczne rozważania przeprowadzić można np. w przypadku operatora biharmonicznego. Rozważmy równanie biharmoniczne
| (12.10) |
Mnożąc obie strony tego równania przez dowolną funkcję![]() i całkując otrzymujemy
i całkując otrzymujemy
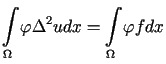 . . |
(12.11) |
Stosując dwukrotnie wzór Greena do lewej strony równości (12.11) możemy napisać, że
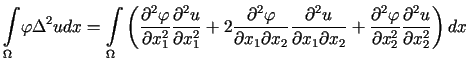
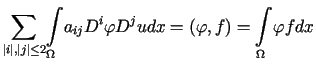 , , |
(12.12) |
gdzie ![]() są takie jak w przykładzie 2.
są takie jak w przykładzie 2.
Podobnie jak w przypadku operatora Laplace'a, możemy sformułować definicję
słabego rozwiązania równania biharmonicznego (12.10)
jako funkcji ![]() spełniającej tożsamość (12.12) dla każdej
funkcji
spełniającej tożsamość (12.12) dla każdej
funkcji ![]() .
.
Sformułujemy teraz ogólną definicję słabego rozwiązania równania różniczkowego ![]() ,
gdzie
,
gdzie ![]() jest operatorem eliptycznym rzędu
jest operatorem eliptycznym rzędu ![]()
D e f i n i c j a
Niech ![]() ,
, ![]() - ograniczone i mierzalne na
- ograniczone i mierzalne na ![]() .
Mówimy, że
.
Mówimy, że ![]() jest słabym rozwiązaniem równania
jest słabym rozwiązaniem równania ![]() ,
gdzie
,
gdzie
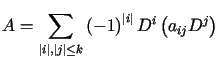 ,
,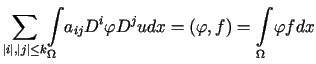 . . |
(12.13) |
D e f i n i c j a
Warunki brzegowe dla równania rzędu ![]() nazywamy stabilnymi wtedy i tylko wtedy gdy nie zawierają one pochodnych
rzędu wyższego niż
nazywamy stabilnymi wtedy i tylko wtedy gdy nie zawierają one pochodnych
rzędu wyższego niż ![]() .
.
Typowym przykładem stabilnego warunku brzegowego jest warunek występujący w zagadnieniu Dirichleta dla równania Laplace'a (k=1)
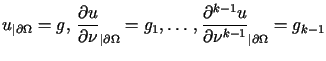 , , |
(12.14) |
gdzie ![]() oznacza wektor normalny zewnętrzny do brzegu
oznacza wektor normalny zewnętrzny do brzegu ![]() .
Warunki te należy rozumieć w sensie śladu, ponieważ funkcje z przestrzeni
.
Warunki te należy rozumieć w sensie śladu, ponieważ funkcje z przestrzeni ![]() wyznaczają na brzegu
wyznaczają na brzegu![]() ślady swoich pochodnych do rzędu
ślady swoich pochodnych do rzędu ![]() włącznie.
włącznie.
U w a g a
Jeżeli ![]() oraz
oraz ![]() w przestrzeni
w przestrzeni ![]() ,
to z ciągłości operatora śladu wynika (patrz nierówność (11.8)),
że
,
to z ciągłości operatora śladu wynika (patrz nierówność (11.8)),
że![]() w
w![]() dla takich wielowskaźników
dla takich wielowskaźników![]() ,
że
,
że ![]() .
W szczególności, jeżeli
.
W szczególności, jeżeli ![]() ,
to
,
to ![]() .
Uzasadnia to przyjętą nazwę stabilnych warunków brzegowych.
.
Uzasadnia to przyjętą nazwę stabilnych warunków brzegowych.
D e f i n i c j a
Warunki brzegowe zawierające pochodne rzędu wyższego niż![]() nazywane są niestabilnymi warunkami brzegowymi dla równania rzędu
nazywane są niestabilnymi warunkami brzegowymi dla równania rzędu ![]() .
.
Warunki niestabilne nie mogą być rozumiane jako ślady funkcji, ponieważ
funkcje z przestrzeni ![]() nie wyznaczają śladów pochodnych rzędu wyższego niż
nie wyznaczają śladów pochodnych rzędu wyższego niż![]() .
Następujący przykład świadczy o tym, że jeśli ciąg funkcji
.
Następujący przykład świadczy o tym, że jeśli ciąg funkcji ![]() zbiega do
zbiega do ![]() w
w ![]() oraz jeśli każda z funkcji
oraz jeśli każda z funkcji ![]() spełnia w sensie śladu pewne warunki brzegowe z pochodnymi rzędu wyższego
niż
spełnia w sensie śladu pewne warunki brzegowe z pochodnymi rzędu wyższego
niż![]() ,
to funkcja graniczna
,
to funkcja graniczna ![]() nie musi spełniać tych warunków (stąd warunki te zwane są niestabilnymi).
nie musi spełniać tych warunków (stąd warunki te zwane są niestabilnymi).
P r z y k ł a d
Niech k=1, ![]() ,
, ![]() ,
,
![\begin{displaymath}u_{n}\left( x\right) =\left\{\begin{array}[c]{lc}%%1-x^{2}......}\right. \text{ \ i przed\l u\.{z}ona do funkcji parzystej.}%%\end{displaymath}](img1680.gif)
 ,
,| (12.15) |
gdzie ![]() jest operatorem eliptycznym rzędu
jest operatorem eliptycznym rzędu ![]() z warunkami brzegowymi, wśród których jest
z warunkami brzegowymi, wśród których jest ![]() warunków stabilnych postaci
warunków stabilnych postaci
Na początek rozważymy kilka szczególnych przypadków zagadnień brzegowych.
| (12.16) |
Niech ![]() .
Przypuśćmy, że
.
Przypuśćmy, że ![]() ,
, ![]() ,
, ![]() jest klasycznym rozwiązaniem zagadnienia (12.16).
Stosując wzór Greena otrzymujemy
jest klasycznym rozwiązaniem zagadnienia (12.16).
Stosując wzór Greena otrzymujemy
 |
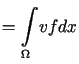 |
|
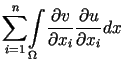 |
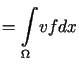 |
(12.17) |
(porównaj wyprowadzenie wzoru (12.9)).
Łatwo zauważyć, ze całki występujące po prawej stronie wzoru (12.17)
są poprawnie określone dla ![]() i
i ![]() .
.
Niech ![]() będzie śladem pewnej funkcji
będzie śladem pewnej funkcji ![]() i niech
i niech ![]() .
Przyjmujemy następującą definicję.
.
Przyjmujemy następującą definicję.
D e f i n i c j a
Funkcję ![]() nazywamy słabym rozwiązaniem zagadnienia (12.16)
wtedy i tylko wtedy gdy
nazywamy słabym rozwiązaniem zagadnienia (12.16)
wtedy i tylko wtedy gdy
Problem istnienia rozwiązania zagadnienia Dirichleta sprowadza się do
tego, czy dana funkcja ![]() jest śladem pewnej funkcji
jest śladem pewnej funkcji ![]() .
Jeśli tak jest, to pokażemy później, że wystarcza to do istnienia rozwiązania.
.
Jeśli tak jest, to pokażemy później, że wystarcza to do istnienia rozwiązania.
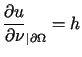 . . |
(12.18) |
Niech ![]() .
Przypuśćmy, że
.
Przypuśćmy, że ![]() ,
,![]() ,
, ![]() jest klasycznym rozwiązaniem zagadnienia (12.18).
Ponieważ
jest klasycznym rozwiązaniem zagadnienia (12.18).
Ponieważ
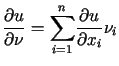 ,
,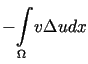 |
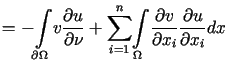 |
|
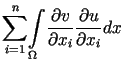 |
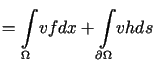 . . |
(12.19) |
Rezygnując z założenia o ciągłości danych funkcji ![]() i
i![]() możemy sformułować definicję.
możemy sformułować definicję.
D e f i n i c j a
Niech ![]() ,
, ![]() .
Słabym rozwiązaniem zagadnienia (12.18)
nazywamy taką funkcję
.
Słabym rozwiązaniem zagadnienia (12.18)
nazywamy taką funkcję ![]() ,
że dla dowolnej funkcji
,
że dla dowolnej funkcji ![]() spełniona jest równość (12.19).
spełniona jest równość (12.19).
U w a g a
Rozwiązania zagadnienia Neumanna nie można zdefiniować za pomocą założenia
o istnieniu takiej funkcji ![]() ,
że
,
że ![]() ,
ponieważ funkcje z przestrzeni
,
ponieważ funkcje z przestrzeni ![]() nie wyznaczają śladów swoich pochodnych pierwszego rzędu na brzegu
nie wyznaczają śladów swoich pochodnych pierwszego rzędu na brzegu![]() .
.
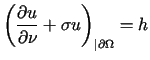 . . |
(12.20) |
Niech ![]() .
Przypuśćmy, że
.
Przypuśćmy, że ![]() ,
,![]() ,
, ![]() jest klasycznym rozwiązaniem zagadnienia (12.20).
Ponieważ
jest klasycznym rozwiązaniem zagadnienia (12.20).
Ponieważ
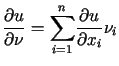 ,
,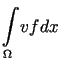 |
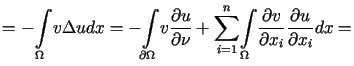 |
|
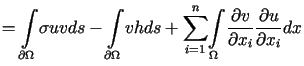 . . |
(12.21) |
Zapiszmy ostatnią równość w postaci
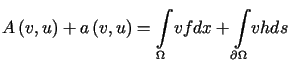 , , |
(12.22) |
gdzie
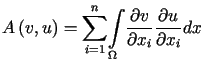 ,
, 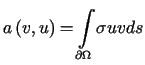 .
.Rezygnując z założenia o ciągłości danych funkcji ![]() i
i![]() możemy sformułować definicję.
możemy sformułować definicję.
D e f i n i c j a
Niech ![]() ,
, ![]() ,
, ![]() .
Słabym rozwiązaniem zagadnienia (12.20)
nazywamy taką funkcję
.
Słabym rozwiązaniem zagadnienia (12.20)
nazywamy taką funkcję ![]() ,
że dla dowolnej funkcji
,
że dla dowolnej funkcji ![]() spełniona jest równość (12.22).
spełniona jest równość (12.22).
Rozważmy równanie
| (12.23) |
gdzie ![]() jest operatorem eliptycznym rzędu
jest operatorem eliptycznym rzędu ![]() postaci (12.1) z warunkami brzegowymi, wśród
których jest
postaci (12.1) z warunkami brzegowymi, wśród
których jest ![]() warunków stabilnych postaci
warunków stabilnych postaci
| (12.24) |
(![]() ,
, ![]() są pewnymi operatorami różniczkowymi rzędu co najwyżej
są pewnymi operatorami różniczkowymi rzędu co najwyżej ![]() ).
Oprócz tego dane jest
).
Oprócz tego dane jest ![]() warunków brzegowych niestabilnych, scharakteryzowanych przez funkcje
warunków brzegowych niestabilnych, scharakteryzowanych przez funkcje ![]() ,
, ![]() .
.
Niech
| (12.25) |
Niech 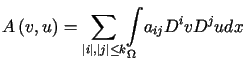 oraz
oraz ![]() będzie brzegową ciągłą formą dwuliniową określoną na
będzie brzegową ciągłą formą dwuliniową określoną na![]() .
.
Niech ![]() będzie taką funkcją, że
będzie taką funkcją, że
| (12.26) |
D e f i n i c j a (przypadek ogólny)
Mówimy, że ![]() jest słabym rozwiązaniem zagadnienia brzegowego określonego przez powyższe
dane wtedy i tylko wtedy gdy
jest słabym rozwiązaniem zagadnienia brzegowego określonego przez powyższe
dane wtedy i tylko wtedy gdy ![]() oraz dla każdej funkcji
oraz dla każdej funkcji ![]() zachodzi tożsamość
zachodzi tożsamość
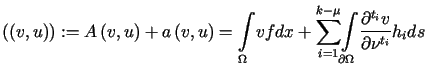 . . |
(12.27) |