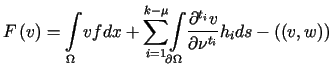D e f i n i c j a
Niech dana będzie przestrzeń Hilberta ![]() i dwuliniowa forma
i dwuliniowa forma ![]() określona na tej przestrzeni. Mówimy, że forma
określona na tej przestrzeni. Mówimy, że forma ![]() jest
jest ![]() eliptyczna
wtedy i tylko wtedy gdy istnieje stała
eliptyczna
wtedy i tylko wtedy gdy istnieje stała ![]() taka, że dla każdej funkcji
taka, że dla każdej funkcji ![]() zachodzi nierówność
zachodzi nierówność
| (12.28) |
T w i e r d z e n i e (Laxa-Milgrama)
Niech ![]() będzie przestrzenią Hilberta z iloczynem skalarnym
będzie przestrzenią Hilberta z iloczynem skalarnym ![]() .
Niech
.
Niech ![]() będzie formą dwuliniową określoną na
będzie formą dwuliniową określoną na ![]() taką, że
taką, że
| (12.29) |
Wówczas każdy funkcjonał liniowy ![]() ograniczony na
ograniczony na ![]() może być przedstawiony w formie
może być przedstawiony w formie
| (12.30) |
gdzie element ![]() jest jednoznacznie wyznaczony przez funkcjonał
jest jednoznacznie wyznaczony przez funkcjonał ![]() .
Ponadto zachodzi nierówność
.
Ponadto zachodzi nierówność
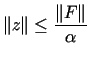 . . |
(12.31) |
Dowód twierdzenia oparty jest na zastosowaniu twierdzenia Riesza dla
reprezentacji funkcjonału liniowego w przestrzeniach Hilberta.
T w i e r d z e n i e (o istnieniu i jednoznaczności rozwiązania zagadnienia brzegowego)
Niech zgodnie z definicją słabego rozwiązania (12.27)
dane będzie zagadnienie brzegowe dla operatora eliptycznego rzędu ![]() .
Jeśli forma
.
Jeśli forma ![]() jest
jest ![]() eliptyczna
wtedy dany problem posiada dokładnie jedno słabe rozwiązanie
eliptyczna
wtedy dany problem posiada dokładnie jedno słabe rozwiązanie ![]() i istnieje stała
i istnieje stała ![]() niezależna od
niezależna od ![]() i
i ![]() taka, że
taka, że
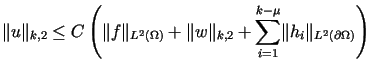 . . |
(12.32) |
Dowód istnienia rozwiązania polega na zastosowaniu twierdzenia Laxa-Milgrama
do funkcjonału ![]() postaci
postaci