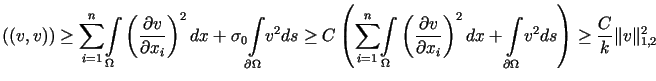Next:Elementy
rachunku wariacyjnegoUp:Rozwiązania
uogólnione (słabe)Previous:Istnienie
słabych rozwiązań zagadnieńSpis
rzeczy
Subsections
Przykłady zagadnień brzegowych
- analiza rozwiązalności
Zagadnienie Dirichleta dla równania
Poissona
Rozważamy zagadnienie (ze stabilnym warunkiem brzegowym)
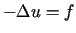 ,
dla
,
dla 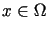 ,
, 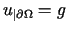 .
Niech
.
Niech 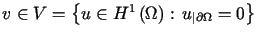 ,
, 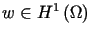 taka, że
taka, że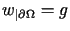 .
Wtedy z (12.17) wynika, że
.
Wtedy z (12.17) wynika, że 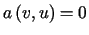 oraz
oraz
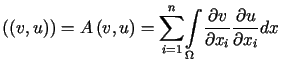 .
Forma
.
Forma 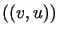 jest
jest 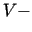 eliptyczna,
ponieważ dla dowolnej funkcji
eliptyczna,
ponieważ dla dowolnej funkcji 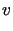 z przestrzeni
z przestrzeni 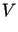 ,
na mocy nierówności Friedrichsa (11.10)
prawdziwe jest oszacowanie postaci
,
na mocy nierówności Friedrichsa (11.10)
prawdziwe jest oszacowanie postaci
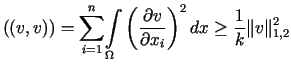 dla pewnej stałej dodatniej
dla pewnej stałej dodatniej 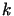 .
.
W takim razie z istnienia funkcji 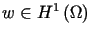 takiej, że jej śladem na brzegu
takiej, że jej śladem na brzegu 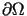 jest
jest 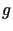 ,
wynika istnienie i jednoznaczność rozwiązania tego zagadnienia.
,
wynika istnienie i jednoznaczność rozwiązania tego zagadnienia.
Zagadnienie Neumanna dla równania
Poissona
Rozważmy zagadnienie (z niestabilnym warunkiem brzegowym)
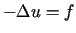 ,
dla
,
dla 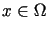 ,
, 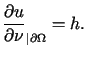 Niech
Niech 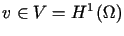 .
Wtedy
.
Wtedy 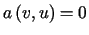 oraz
oraz
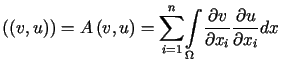 .
W tym przypadku forma
.
W tym przypadku forma 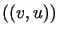 nie jest
nie jest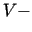 eliptyczna,
ponieważ dla
eliptyczna,
ponieważ dla 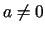 funkcja stała
funkcja stała 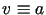 spełnia warunek
spełnia warunek 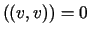 ,
ale
,
ale 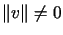 .
Oznacza to, że nie można stosować twierdzenia o istnieniu i jednoznaczności
rozwiązania zagadnienia brzegowego.
.
Oznacza to, że nie można stosować twierdzenia o istnieniu i jednoznaczności
rozwiązania zagadnienia brzegowego.
Wykazanie rozwiązalności zagadnienia Neumanna wymaga przyjęcia pewnych
dodatkowych założeń, których nie będziemy w tym miejscu omawiać. W przypadku
klasycznym warunkiem tym jest równość (7.24).
Zagadnienie Newtona dla równania
Poissona
Rozważmy zagadnienie (z niestabilnym warunkiem brzegowym)
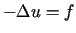 ,
dla
,
dla 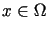 ,
, 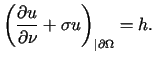 Niech
Niech 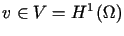 .
Wtedy, zgodnie z równością (12.22)
.
Wtedy, zgodnie z równością (12.22)
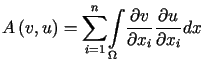 ,
, 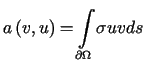 ,
zatem
,
zatem
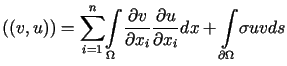 .
Załóżmy ponadto, że we wszystkich punktach
.
Załóżmy ponadto, że we wszystkich punktach  spełniona jest nierówność
spełniona jest nierówność  .
Oznaczając
.
Oznaczając  i stosując nierówność Friedrichsa (11.10)
otrzymujemy
i stosując nierówność Friedrichsa (11.10)
otrzymujemy
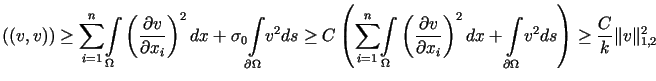 co dowodzi
co dowodzi  eliptyczności
formy
eliptyczności
formy  .
Oznacza to, że rozważany problem posiada jednoznaczne rozwiązanie.
.
Oznacza to, że rozważany problem posiada jednoznaczne rozwiązanie.




Next:Elementy
rachunku wariacyjnegoUp:Rozwiązania
uogólnione (słabe)Previous:Istnienie
słabych rozwiązań zagadnieńSpis
rzeczy
Administrator 2003-03-17
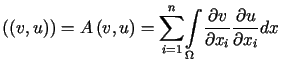 .
.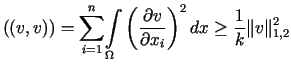
![]() takiej, że jej śladem na brzegu
takiej, że jej śladem na brzegu ![]() jest
jest ![]() ,
wynika istnienie i jednoznaczność rozwiązania tego zagadnienia.
,
wynika istnienie i jednoznaczność rozwiązania tego zagadnienia.
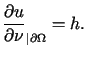
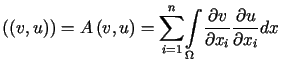 .
.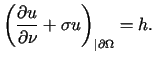
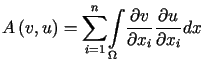 ,
, 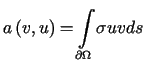 ,
,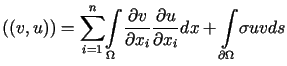 .
.