



Next:Warunek
konieczny istnienia ekstremumUp:Elementy
rachunku wariacyjnegoPrevious:Elementy
rachunku wariacyjnegoSpis
rzeczy
Subsections
Przykładowe zagadnienia
Rachunek wariacyjny zajmuje się metodami wyznaczania wartości ekstremalnych
funkcjonałów określonych na pewnych przestrzeniach funkcyjnych. Klasyczna
teoria rachunku wariacyjnego pochodzi od Eulera (1707-1783). Poniżej przedstawimy
kilka przykładowych problemów prowadzących do zagadnień wariacyjnych.
Zagadnienie brachistochrony
W roku 1696 Johann Bernoulli postawił następujący problem.
Dane są dwa ustalone punkty 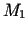 i
i 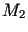 nie
leżące na pionowej prostej. Należy wyznaczyć linię - drogę, po której punkt
materialny zsunie się od
nie
leżące na pionowej prostej. Należy wyznaczyć linię - drogę, po której punkt
materialny zsunie się od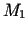 do
do 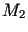 w najkrótszym czasie pod wpływem siły ciążenia, zakładając, że prędkość
początkowa w punkcie
w najkrótszym czasie pod wpływem siły ciążenia, zakładając, że prędkość
początkowa w punkcie 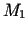 jest
równa zeru.
jest
równa zeru.
Niech 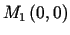 ,
, 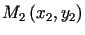 .
Zakładając, że szukana krzywa dana jest równaniem
.
Zakładając, że szukana krzywa dana jest równaniem 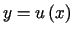 wnioskujemy, że muszą być spełnione warunki brzegowe
wnioskujemy, że muszą być spełnione warunki brzegowe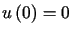 ,
, 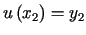 .
Z zasady zachowania energii wynika, że
.
Z zasady zachowania energii wynika, że
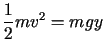 ,
zatem
,
zatem
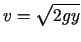 .
Ponieważ
.
Ponieważ
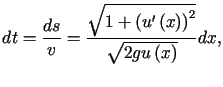 więc całkowity czas zsuwania się punktu materialnego po krzywej
więc całkowity czas zsuwania się punktu materialnego po krzywej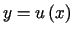 można zapisać wzorem
można zapisać wzorem
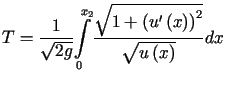 . . |
(13.1) |
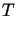 jest funkcjonałem
postaci
jest funkcjonałem
postaci 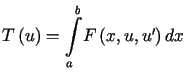 .
Należy wyznaczyć taką funkcję
.
Należy wyznaczyć taką funkcję 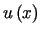 ,
dla której wyrażenie (13.1) przyjmuje wartość
minimalną
w klasie funkcji różniczkowalnych spełniających zadane warunki brzegowe
,
dla której wyrażenie (13.1) przyjmuje wartość
minimalną
w klasie funkcji różniczkowalnych spełniających zadane warunki brzegowe 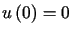 ,
, 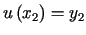 .
.
Powierzchnia obrotowa o minimalnym
polu
Postawmy zagadnienie wyznaczenia funkcji 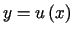 ,
która spełnia warunki brzegowe
,
która spełnia warunki brzegowe 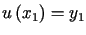 ,
, 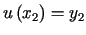 takiej, że pole powierzchni obrotowej otrzymanej przez obrót tej krzywej
dookoła osi
takiej, że pole powierzchni obrotowej otrzymanej przez obrót tej krzywej
dookoła osi 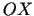 w przedziale
w przedziale ![$ \left[x_{1};x_{2}\right] $](img1791.gif) jest minimalne. Ponieważ pole powierzchni obrotowej opisane jest wzorem
jest minimalne. Ponieważ pole powierzchni obrotowej opisane jest wzorem
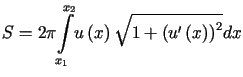 , , |
(13.2) |
więc zagadnienie powyższe prowadzi do minimalizacji funkcjonału (13.2).
Powierzchnia o minimalnym polu
przechodząca przez daną krzywą
Niech 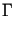 będzie
daną krzywą zamkniętą w
będzie
daną krzywą zamkniętą w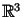 .
Poszukujemy powierzchni
.
Poszukujemy powierzchni 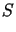 ,
której brzegiem jest
,
której brzegiem jest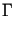 ,
i której pole jest minimalne. Analitycznie oznacza to, że szukamy funkcji
dwóch zmiennych
,
i której pole jest minimalne. Analitycznie oznacza to, że szukamy funkcji
dwóch zmiennych 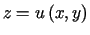 spełniającej warunek brzegowy
spełniającej warunek brzegowy
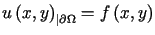 ,
gdzie
,
gdzie 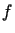 jest dana, a
jest dana, a 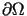 jest rzutem
jest rzutem 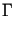 na płaszczyznę
na płaszczyznę 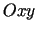 ,
takiej, że funkcjonał
,
takiej, że funkcjonał
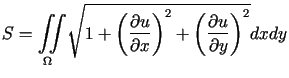 |
(13.3) |
przyjmuje wartość minimalną (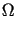 jest obszarem, którego brzegiem jest
jest obszarem, którego brzegiem jest 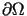 ).
Rozważany funkcjonał (13.3) jest postaci
).
Rozważany funkcjonał (13.3) jest postaci 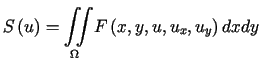 .
.




Next:Warunek
konieczny istnienia ekstremumUp:Elementy
rachunku wariacyjnegoPrevious:Elementy
rachunku wariacyjnegoSpis
rzeczy
Administrator 2003-04-06
![]() i
i ![]() nie
leżące na pionowej prostej. Należy wyznaczyć linię - drogę, po której punkt
materialny zsunie się od
nie
leżące na pionowej prostej. Należy wyznaczyć linię - drogę, po której punkt
materialny zsunie się od![]() do
do ![]() w najkrótszym czasie pod wpływem siły ciążenia, zakładając, że prędkość
początkowa w punkcie
w najkrótszym czasie pod wpływem siły ciążenia, zakładając, że prędkość
początkowa w punkcie ![]() jest
równa zeru.
jest
równa zeru.
![]() ,
, ![]() .
Zakładając, że szukana krzywa dana jest równaniem
.
Zakładając, że szukana krzywa dana jest równaniem ![]() wnioskujemy, że muszą być spełnione warunki brzegowe
wnioskujemy, że muszą być spełnione warunki brzegowe![]() ,
, ![]() .
Z zasady zachowania energii wynika, że
.
Z zasady zachowania energii wynika, że
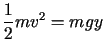 ,
,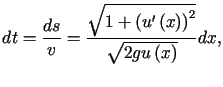
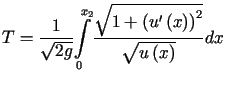 .
.![]() jest funkcjonałem
postaci
jest funkcjonałem
postaci 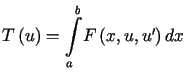 .
Należy wyznaczyć taką funkcję
.
Należy wyznaczyć taką funkcję ![]() ,
dla której wyrażenie (13.1) przyjmuje wartość
minimalną
w klasie funkcji różniczkowalnych spełniających zadane warunki brzegowe
,
dla której wyrażenie (13.1) przyjmuje wartość
minimalną
w klasie funkcji różniczkowalnych spełniających zadane warunki brzegowe ![]() ,
, ![]() .
.
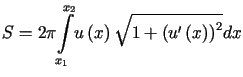 ,
,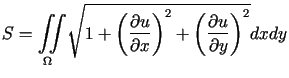
![]() jest obszarem, którego brzegiem jest
jest obszarem, którego brzegiem jest ![]() ).
Rozważany funkcjonał (13.3) jest postaci
).
Rozważany funkcjonał (13.3) jest postaci 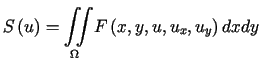 .
.