D e f i n i c j a
Mówimy, że funkcjonał ![]() jest różniczkowalny w punkcie
jest różniczkowalny w punkcie ![]() wtedy i tylko wtedy gdy przyrost
wtedy i tylko wtedy gdy przyrost ![]() daje się przedstawić w postaci
daje się przedstawić w postaci
| (13.4) |
gdzie ![]() jest funkcjonałem liniowym względem
jest funkcjonałem liniowym względem ![]() ,
oraz
,
oraz ![]() .
Funkcjonał
.
Funkcjonał ![]() nazywamy wariacją (różniczką w sensie Frécheta) funkcjonału
nazywamy wariacją (różniczką w sensie Frécheta) funkcjonału ![]() .
Wariację
.
Wariację ![]() zapisujemy symbolicznie jako
zapisujemy symbolicznie jako ![]() .
.
Pojęcie wariacji funkcjonału pozwala sformułować w prosty sposób warunek konieczny istnienia ekstremum funkcjonału.
T w i e r d z e n i e
Jeśli funkcjonał ![]() posiada ekstremum dla
posiada ekstremum dla ![]() oraz istnieje wariacja funkcjonału
oraz istnieje wariacja funkcjonału ![]() ,
to
,
to
| (13.5) |
Dla dowodu wystarczy zauważyć, że ![]() .
Ponieważ
.
Ponieważ ![]() dla
dla ![]() ,
więc znak wyrażenia
,
więc znak wyrażenia ![]() dla dostatecznie małych
dla dostatecznie małych ![]() określony jest przez znak pierwszego składnika. Gdyby
określony jest przez znak pierwszego składnika. Gdyby ![]() ,
z liniowości wariacji
,
z liniowości wariacji ![]() wynika, że dla małych
wynika, że dla małych ![]() znak ten może być zarówno dodatni jak i ujemny, zatem funkcjonał
znak ten może być zarówno dodatni jak i ujemny, zatem funkcjonał ![]() nie może osiągać ekstremum w punkcie
nie może osiągać ekstremum w punkcie ![]() .
.
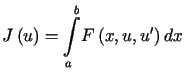 |
(13.6) |
w przestrzeni ![]() .
.
Niech ![]() będzie przyrostem funkcji
będzie przyrostem funkcji ![]() ,
tzn.
,
tzn. ![]() oraz
oraz ![]() .
Wynika stąd, że
.
Wynika stąd, że
Wyznaczmy wariację ![]() .
Mamy
.
Mamy
![$\displaystyle \Delta J=%%{\displaystyle\int\limits_{a}^{b}}F\left( x,u+h,u^{\......\prime}+h^{\prime}\right) -F\left( x,u,u^{\prime}\right) \right] dx\text{.}%%$](img1828.gif)
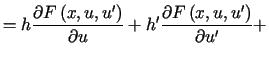 |
||
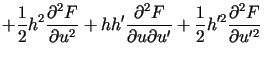 , , |
gdzie pochodne ![]() ,
, ![]() ,
, ![]() obliczone są w punkcie
obliczone są w punkcie ![]() ,
, ![]() .
.
W takim razie
![$\displaystyle \Delta J=<tex2html_comment_mark>2458 {\displaystyle\int\limits_{a......e}\right) }{\partial u^{\prime}}\right] dx+\alpha\left( u,h\right) \Vert h\Vert$](img1837.gif) , , |
(13.7) |
gdzie
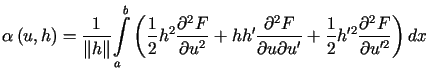 . . |
(13.8) |
Szacując wyrażenie (13.8) otrzymujemy
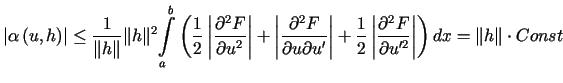
![$\displaystyle \delta J\left( h\right) =<tex2html_comment_mark>2474 {\displaysty......e}\frac{\partial F\left( x,u,u^{\prime}\right) }{\partial u^{\prime}}\right] dx$](img1841.gif) . . |
(13.9) |
Zgodnie ze wzorem (13.5) warunkiem koniecznym
istnienia ekstremum funkcjonału jest spełnianie warunku ![]() .
Całkując przez części drugi składnik we wzorze (13.9)
otrzymujemy
.
Całkując przez części drugi składnik we wzorze (13.9)
otrzymujemy
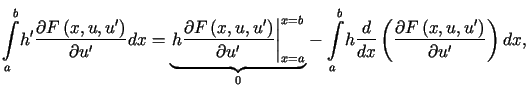
![$\displaystyle \delta J\left( h\right) =%%{\displaystyle\int\limits_{a}^{b}}h\......\frac{d}{dx}F_{u^{\prime}%%}\left( x,u,u^{\prime}\right) \right] dx\text{.}%%$](img1844.gif)
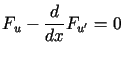 . . |
(13.10) |
Równanie to nosi nazwę równania Eulera. Jest to właśnie warunek
konieczny istnienia ekstremum funkcjonału postaci (13.6).
Rozwiązania równania Eulera nazywają się
ekstremalami. Z udowodnionego
uprzednio twierdzenia wynika, że funkcjonał ![]() może posiadać ekstrema tylko na zbiorze ekstremal, zależy to jednak od
spełnienia pewnych warunków dostatecznych istnienia ekstremum. Warunków
tych nie będziemy w tym miejscu omawiać.
może posiadać ekstrema tylko na zbiorze ekstremal, zależy to jednak od
spełnienia pewnych warunków dostatecznych istnienia ekstremum. Warunków
tych nie będziemy w tym miejscu omawiać.
P r z y k ł a d 1 (zagadnienie brachistochrony)
Rozważmy funkcjonał opisany wzorem (13.1). Jest on postaci
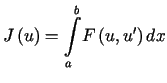
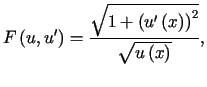
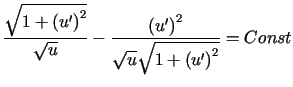 . . |
(13.11) |
Wprowadzając parametr ![]() można zapisać rozwiązanie równania (13.11)
w postaci parametrycznej
można zapisać rozwiązanie równania (13.11)
w postaci parametrycznej
P r z y k ł a d 2 (powierzchnia obrotowa o minimalnym polu)
Zagadnienie znalezienia powierzchni obrotowej o minimalnym polu przechodzącej przez ustalone punkty równoważne jest minimalizacji funkcjonału (13.2). Ponieważ
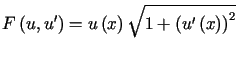
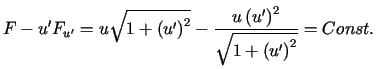
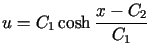 ,
,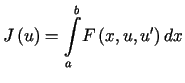
| (13.12) |
Warunki te spełnia każda krzywa, na której realizowane jest ekstremum
funkcjonału ![]() .
.
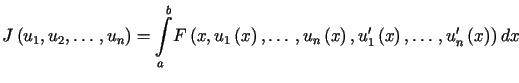 |
(13.13) |
przy założeniu, że funkcje ![]() spełniają pewne warunki brzegowe dla
spełniają pewne warunki brzegowe dla ![]() i
i ![]() .
.
Wykorzystując rozwinięcie funkcji ![]() za pomocą wzoru Taylora, można pokazać, że w tym przypadku wariacja
za pomocą wzoru Taylora, można pokazać, że w tym przypadku wariacja ![]() funkcjonału (13.13) dana jest wzorem
funkcjonału (13.13) dana jest wzorem
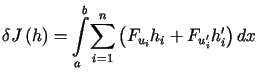 . . |
(13.14) |
Wzór ten jest uogólnieniem wzoru (13.9).
Dobierając w sposób niezależny funkcje ![]() łatwo pokazać, że warunek powyższy prowadzi do układu równań Eulera postaci
łatwo pokazać, że warunek powyższy prowadzi do układu równań Eulera postaci
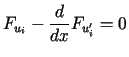 dla
dla |
(13.15) |
P r z y k ł a d (zasada najmniejszego działania)
Załóżmy, że dany jest pewien układ punktów materialnych o masach ![]() i współrzędnych
i współrzędnych ![]() dla
dla ![]() .
Zakładamy, że układowi temu nie nałożono żadnych więzów.
.
Zakładamy, że układowi temu nie nałożono żadnych więzów.
Energia kinetyczna układu wyraża się wzorem
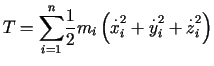 .
.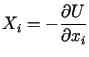 ,
, 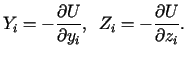
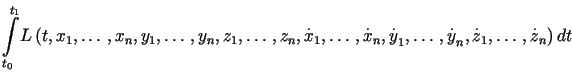 . . |
(13.16) |
Na mocy układu równań Eulera (13.15) zastosowanego do funkcji
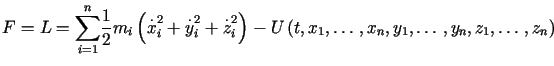
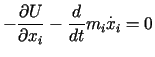 ,
, 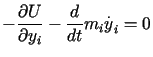 ,
, 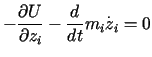 dla
dla | (13.17) |
Równania (13.17) sa równaniami ruchu
dla układu ![]() punktów
materialnych.
punktów
materialnych.
Udowodniliśmy w ten sposób następującą zasadę najmniejszego działania.
Ruch układu w przedziale czasowym ![]() opisują te funkcje
opisują te funkcje ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
dla których całka (13.16) osiąga
minimum.
,
dla których całka (13.16) osiąga
minimum.
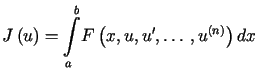 |
(13.18) |
z warunkami brzegowymi
| (13.19) |
Rozumując analogicznie jak w poprzednich przypadkach można pokazać,
że wariacja ![]() wyraża się wzorem
wyraża się wzorem
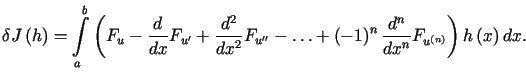
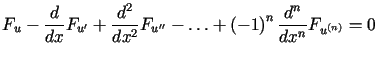 . . |
(13.20) |
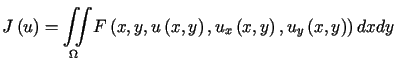 |
(13.21) |
osiąga wartość ekstremalną. Od funkcji ![]() wymagamy, aby spełniała warunek brzegowy postaci
wymagamy, aby spełniała warunek brzegowy postaci
| (13.22) |
gdzie ![]() jest daną funkcją określoną na brzegu
jest daną funkcją określoną na brzegu![]() .
.
Zakładając, że ![]() jest klasy
jest klasy ![]() i analizując postać przyrostu
i analizując postać przyrostu ![]() można wyprowadzić następujący wzór na wariację funkcjonału
można wyprowadzić następujący wzór na wariację funkcjonału
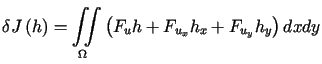 . . |
(13.23) |
Przekształcając wzór (13.23) za pomocą
wzoru Greena i zakładając, że ![]() ,
otrzymujemy ostatecznie, że
,
otrzymujemy ostatecznie, że
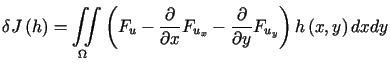 . . |
(13.24) |
Wynika stąd następujące równanie Eulera
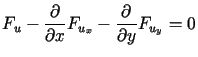 . . |
(13.25) |
Równanie (13.25) wraz z warunkiem brzegowym ![]() jest sformułowaniem warunku koniecznego dla istnienia ekstremum funkcjonału
(13.21). Jest to równanie różniczkowe cząstkowe.
jest sformułowaniem warunku koniecznego dla istnienia ekstremum funkcjonału
(13.21). Jest to równanie różniczkowe cząstkowe.
P r z y k ł a d 1
Rozważmy funkcjonał
![$\displaystyle J\left( u\right) =<tex2html_comment_mark>2592 {\displaystyle\iint...... x}\right) ^{2}+\left( \frac{\partial u}{\partial y}\right) ^{2}\right] dxdy%%$](img1903.gif) |
(13.26) |
z warunkiem brzegowym ![]() .
.
W tym przypadku
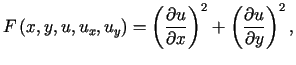
| (13.27) |
Oznacza to, ze funkcja ![]() jest rozwiązaniem zagadnienia Dirichleta dla równania Laplace'a.
jest rozwiązaniem zagadnienia Dirichleta dla równania Laplace'a.
Łatwo pokazać, ze funkcja ![]() będąca rozwiązaniem zagadnienia (13.27)
realizuje minimum funkcjonału (13.26).
będąca rozwiązaniem zagadnienia (13.27)
realizuje minimum funkcjonału (13.26).
Niech ![]() ,
gdzie
,
gdzie ![]() .
Wówczas
.
Wówczas
![$\displaystyle =J\left( u_{0}+h\right) =<tex2html_comment_mark>2600 {\displaysty......rtial u_{0}}{\partial y}+\frac{\partial h}{\partial y}\right) ^{2}\right] dxdy=$](img1908.gif) |
||
![$\displaystyle =<tex2html_comment_mark>2604 {\displaystyle\iint\limits_{\Omega}}......al x}\right) ^{2}+\left( \frac{\partial h}{\partial y}\right) ^{2}\right] dxdy+$](img1909.gif) |
||
![$\displaystyle +2{\displaystyle\iint\limits_{\Omega}} \left[ \frac{\partial u_{0......616 +\frac{\partial u_{0}}{\partial y}\frac{\partial h}{\partial y}\right] dxdy$](img1910.gif) . . |
Stosując twierdzenie Greena i uwzględniając fakt, że ![]() łatwo pokazać, że
łatwo pokazać, że
![$\displaystyle %%{\displaystyle\iint\limits_{\Omega}}\left[ \frac{\partial u_{......%+\frac{\partial u_{0}}{\partial y}\frac{\partial h}{\partial y}\right]dxdy=0$](img1912.gif) ,
,![$\displaystyle J\left( u_{0}+h\right) =J\left( u_{0}\right) +%%{\displaystyle\i......\frac{\partial h}{\partial y}\right) ^{2}\right] dxdy\geq J\left(u_{0}\right)$](img1913.gif)
P r z y k ł a d 2
Rozważmy funkcjonał
![$\displaystyle J\left( u\right) =<tex2html_comment_mark>2629 {\displaystyle\iint...... \frac{\partial u}{\partial y}\right) ^{2}+2uf\left( x,y\right) \right] dxdy%%$](img1914.gif) |
(13.28) |
z warunkiem brzegowym ![]() .
.
W tym przypadku
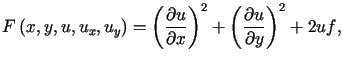
| (13.29) |
Jest to zagadnienie Dirichleta dla równania Poissona.
P r z y k ł a d 3
Zagadnienie znajdowania powierzchni o minimalnym polu przechodzącej
przez daną krzywą w przestrzeni ![]() prowadzi do poszukiwania minimum funkcjonału
prowadzi do poszukiwania minimum funkcjonału
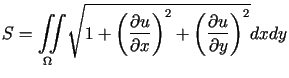 |
(13.30) |
z warunkiem ![]() .
.
W tym przypadku równanie Eulera (13.25) przybiera postać
![$\displaystyle \left[ 1+\left( \frac{\partial u}{\partial y}\right) ^{2}\right] ......artial u}{\partial x}\right) ^{2}\right] \frac{\partial^{2}u}{\partial y^{2}}=0$](img1918.gif) . . |
(13.31) |
Fizycznie powierzchnię o minimalnym polu realizuje powierzchnia bańki
mydlanej przechodzącej przez zadaną krzywą w przestrzeni.
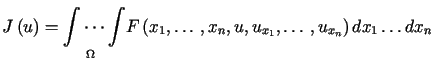 |
(13.32) |
równanie Eulera przybiera postać
 . . |
(13.33) |
Podobnie dla funkcjonału
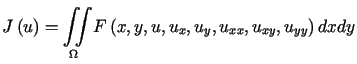 |
(13.34) |
można wyprowadzić następujące równanie Eulera
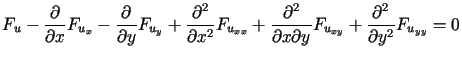 . . |
(13.35) |
Przykładowo dla funkcjonału
![$\displaystyle J\left( u\right) =%%{\displaystyle\iint\limits_{\Omega}}\left[ ......ial^{2}u}{\partial x\partial y}\right) ^{2}-2uf\left( x,y\right) \right] dxdy$](img1923.gif)