Next:ZadaniaUp:Pojęcia
podstawowePrevious:Zagadnienie
Cauchy'ego dla równaniaSpis
rzeczy
Zagadnienia graniczne poprawnie
postawione
Dla równań różniczkowych cząstkowych rozważamy zwykle tzw. zagadnienia
graniczne polegające na znalezieniu rozwiązania równania spełniającego
pewne dodatkowe warunki -
warunki początkowe (określone w pewnej
chwili czasu np. 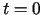 )
lub/i warunki brzegowe (określone zwykle na brzegu rozważanego obszaru
przestrzennego). Warunki te nazywamy ogólnie
warunkami granicznymi.
)
lub/i warunki brzegowe (określone zwykle na brzegu rozważanego obszaru
przestrzennego). Warunki te nazywamy ogólnie
warunkami granicznymi.
D e f i n i c j a
Mówimy, że zagadnienie graniczne jest poprawnie postawione, jeżeli:
-
-przy określonych warunkach granicznych istnieje rozwiązanie tego zagadnienia,
-
-rozwiązanie to jest jednoznaczne,
-
-rozwiązanie to zależy w sposób ciągły od zadanych warunków granicznych
(jest stabilne).
Sens trzeciego warunku powyższej definicji polega na tym, że gdyby w modelu
matematycznym opisującym zjawisko fizyczne nie było ciągłej zależności
rozwiązania od warunków granicznych zadania, to praktycznie dwa jednakowe
układy warunków (tj. takie, ze różnice między nimi mieszczą się w granicach
błędów pomiarowych) mogłyby odpowiadać dwóm istotnie różnym przebiegom
zjawiska. Oznacza to, że zjawisko nie byłoby wyznaczalne fizycznie.
Nie każde zagadnienie graniczne dla równania różniczkowego cząstkowego
jest poprawnie postawione. Przykładem zagadnienia, które nie jest zagadnieniem
poprawnie postawionym może być np. następujące zagadnienie.
P r z y k ł a d
Wyznaczyć funkcję 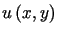 spełniającą równanie Laplace'a
spełniającą równanie Laplace'a
Z teorii funkcji zmiennej zespolonej wynika, że powyższe zagadnienie
posiada jednoznaczne rozwiązanie. Łatwo zauważyć, że funkcja
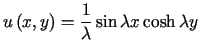 dla dowolnej wartości parametru
dla dowolnej wartości parametru 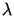 jest rozwiązaniem powyższego zagadnienia dla
jest rozwiązaniem powyższego zagadnienia dla 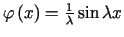 i
i 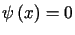 .
Ponieważ dla dużych wartości
.
Ponieważ dla dużych wartości 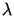 warunki graniczne różnią się dowolnie mało od zera, więc gdyby zagadnienie
było stabilne, to również rozwiązanie powinno być bliskie zeru, ale tak
nie jest.
warunki graniczne różnią się dowolnie mało od zera, więc gdyby zagadnienie
było stabilne, to również rozwiązanie powinno być bliskie zeru, ale tak
nie jest.
Należy pamiętać, że mówiąc o stabilności zagadnienia trzeba najpierw
precyzyjnie określić co to znaczy, że rozwiązanie zagadnienia zależy w
sposób ciągły od warunków granicznych.




Next:ZadaniaUp:Pojęcia
podstawowePrevious:Zagadnienie
Cauchy'ego dla równaniaSpis
rzeczy
Administrator 2003-02-13
![]() spełniającą równanie Laplace'a
spełniającą równanie Laplace'a