



Next:Zagadnienia
graniczne poprawnie postawioneUp:Pojęcia
podstawowePrevious:Uwagi
o klasyfikacji liniowychSpis
rzeczy
Zagadnienie Cauchy'ego dla równania
liniowego
Rozważmy liniowe r.r.cz. rzędu 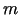 postaci
postaci
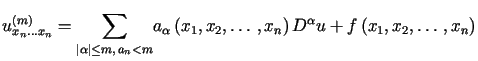 |
(1.14) |
w obszarze 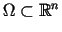 ,
który ma niepuste przecięcie z płaszczyzną
,
który ma niepuste przecięcie z płaszczyzną 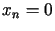 .
.
Zagadnieniem Cauchy'ego (zagadnieniem początkowym) dla równania
(1.14) nazywamy zagadnienie polegające na wyznaczeniu
rozwiązania tego równania spełniającego jednocześnie następujące warunki
początkowe
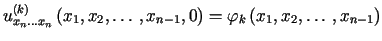 dla
dla 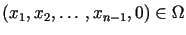 |
(1.15) |
i 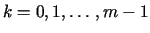 .
.
Następujące twierdzenie określa warunki wystarczające istnienia lokalnego
rozwiązania powyższego zagadnienia początkowego.
T w i e r d z e n i e (Cauchy'ego-Kowalewskiej)
Jeżeli:
-
-
współczynniki
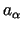 i wyraz wolny
i wyraz wolny 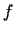 w równaniu (1.14) są funkcjami analitycznymi
w obszarze
w równaniu (1.14) są funkcjami analitycznymi
w obszarze 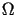 ,
,
-
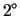
-
funkcje
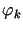 (
(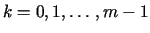 )
są analityczne w obszarze
)
są analityczne w obszarze 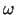 będącym przecięciem
będącym przecięciem 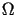 i płaszczyzny
i płaszczyzny 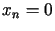 ,
,
to zagadnienie Cauchy'ego (1.14)-(1.15)
ma dokładnie jedno rozwiązanie analityczne, określone w pewnym otoczeniu 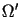 obszaru
obszaru 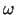 .
Obszar
.
Obszar 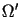 zależy od obszaru analityczności danych funkcji.
zależy od obszaru analityczności danych funkcji.




Next:Zagadnienia
graniczne poprawnie postawioneUp:Pojęcia
podstawowePrevious:Uwagi
o klasyfikacji liniowychSpis
rzeczy
Administrator 2003-02-13
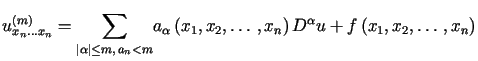
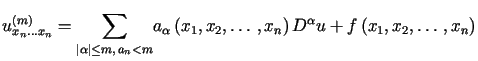
![]() ,
który ma niepuste przecięcie z płaszczyzną
,
który ma niepuste przecięcie z płaszczyzną ![]() .
.
![]() .
.