



Next:ZadaniaUp:Wstęp
do metod przybliżonychPrevious:Metoda
najmniejszych kwadratówSpis
rzeczy
Metoda gradientów
Metoda ta dotyczy operatorów ograniczonych, dodatnio określonych na pewnym
gęstym podzbiorze 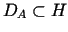 (nie nadaje się więc do operatorów różniczkowych).
(nie nadaje się więc do operatorów różniczkowych).
Niech 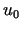 będzie rozwiązaniem uogólnionym równania
będzie rozwiązaniem uogólnionym równania 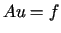 w
w  .
Wówczas
.
Wówczas 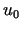 minimalizuje funkcjonał
minimalizuje funkcjonał
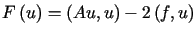 .
Funkcjonał ten, jako funkcjonał ograniczony, określony na podzbiorze gęstym
w
.
Funkcjonał ten, jako funkcjonał ograniczony, określony na podzbiorze gęstym
w  może być przedłużony na całą przestrzeń
może być przedłużony na całą przestrzeń  z zachowaniem ograniczoności.
z zachowaniem ograniczoności.
Niech 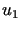 będzie dowolnym elementem przestrzeni
będzie dowolnym elementem przestrzeni  .
Załóżmy, że
.
Załóżmy, że 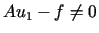 (w przeciwnym razie
(w przeciwnym razie 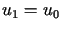 i procedura jest zakończona). Wówczas poszukujemy takiego elementu
i procedura jest zakończona). Wówczas poszukujemy takiego elementu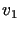 ,
że
,
że
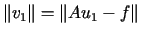 i
i 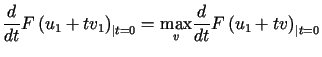 . . |
(14.23) |
Ponieważ
zatem
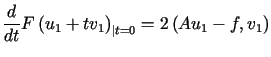 .
Wyrażenie to osiąga wartość największą gdy
.
Wyrażenie to osiąga wartość największą gdy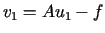 .
Dla wyznaczonego
.
Dla wyznaczonego 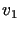 wyrażenie
wyrażenie 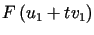 osiąga wartość najmniejszą gdy
osiąga wartość najmniejszą gdy
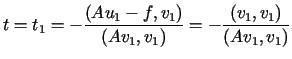 . . |
(14.24) |
Niech teraz 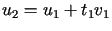 .
Powtarzamy powyższe rozumowanie dla elementu wyjściowego
.
Powtarzamy powyższe rozumowanie dla elementu wyjściowego 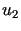 i otrzymujemy
i otrzymujemy
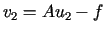 ,
, 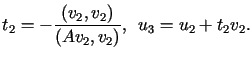 W ten sam sposób można skonstruować rekurencyjnie kolejne elementy ciągu
W ten sam sposób można skonstruować rekurencyjnie kolejne elementy ciągu 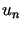 takie, że
takie, że
T w i e r d z e n i e
Jeśli istnieją takie stałe dodatnie 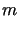 i
i 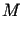 ,
że dla każdego
,
że dla każdego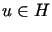 spełniona jest nierówność
spełniona jest nierówność
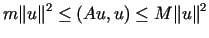 ,
to otrzymany powyżej ciąg
,
to otrzymany powyżej ciąg 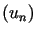 zbiega do rozwiązania uogólnionego
zbiega do rozwiązania uogólnionego 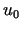 równania
równania 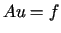 w
w 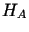 (więc i w
(więc i w  ),
przy czym zachodzi nierówność
),
przy czym zachodzi nierówność
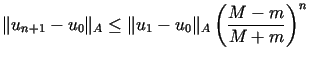 dla
dla 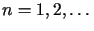 .
.




Next:ZadaniaUp:Wstęp
do metod przybliżonychPrevious:Metoda
najmniejszych kwadratówSpis
rzeczy
Administrator 2003-04-24
![]() będzie dowolnym elementem przestrzeni
będzie dowolnym elementem przestrzeni ![]() .
Załóżmy, że
.
Załóżmy, że ![]() (w przeciwnym razie
(w przeciwnym razie ![]() i procedura jest zakończona). Wówczas poszukujemy takiego elementu
i procedura jest zakończona). Wówczas poszukujemy takiego elementu![]() ,
że
,
że
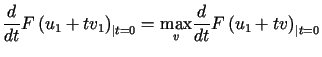 .
.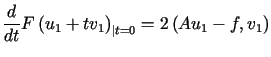 .
.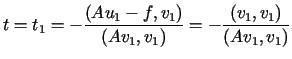 .
.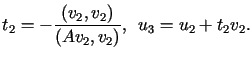
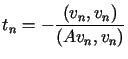 ,
, ![]() i
i ![]() ,
że dla każdego
,
że dla każdego![]() spełniona jest nierówność
spełniona jest nierówność
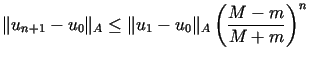 dla
dla