



Next:Metoda
gradientówUp:Wstęp
do metod przybliżonychPrevious:Metoda
GalerkinaSpis
rzeczy
Metoda najmniejszych kwadratów
Niech 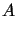 będzie operatorem liniowym określonym na
będzie operatorem liniowym określonym na 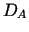 ,
, 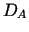 gęsty w
gęsty w  ,
,  - ośrodkowa przestrzeń Hilberta. Załóżmy, że dany jest układ funkcji
- ośrodkowa przestrzeń Hilberta. Załóżmy, że dany jest układ funkcji 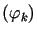 w
w  taki, że
taki, że 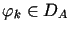 dla
dla 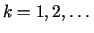 oraz
oraz 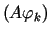 stanowi bazę w
stanowi bazę w  (układ taki nazywamy
(układ taki nazywamy 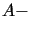 bazą
w
bazą
w  )
)
Metoda najmniejszych kwadratów polega na poszukiwaniu ciągu
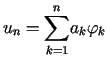 przybliżeń rozwiązania uogólnionego
przybliżeń rozwiązania uogólnionego 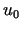 równania
równania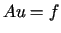 .
Stałe
.
Stałe 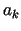 wyznacza się za pomocą warunku
wyznacza się za pomocą warunku
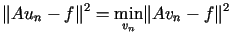 , , |
(14.20) |
gdzie minimum rozpatruje się po wszytkich funkcjach postaci 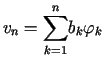 .
.
Obliczając 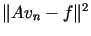 otrzymujemy
otrzymujemy
Wyrażenie to osiąga minimum gdy 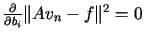 dla
dla 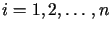 co można zapisać w postaci układu równań
co można zapisać w postaci układu równań
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2934 \left(......varphi _{n}\right) b_{n} & =\left( f,A\varphi_{n}\right) \end{array} \right.%%$](img2100.gif) |
(14.21) |
Z założenia wynika, że wyznacznik układu (14.21)
jest różny od zera, zatem współczynniki 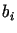 są jednoznacznie wyznaczone.
są jednoznacznie wyznaczone.
T w i e r d z e n i e
Niech 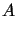 będzie operatorem liniowym dodatnio określonym na
będzie operatorem liniowym dodatnio określonym na 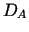 ,
,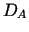 gęsty w
gęsty w  ,
, 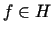 ,
,  - ośrodkowa przestrzeń Hilberta. Niech
- ośrodkowa przestrzeń Hilberta. Niech 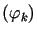 będzie
będzie 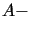 bazą
w
bazą
w  (tzn.
(tzn. 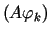 jest bazą w
jest bazą w  )
oraz
)
oraz 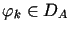 dla
dla 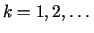 .
Wówczas ciąg
.
Wówczas ciąg 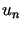 postaci
postaci
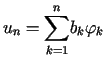 gdzie stałe
gdzie stałe 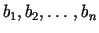 są wyznaczone z układu równań (14.21) jest
zbieżny w
są wyznaczone z układu równań (14.21) jest
zbieżny w 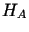 (a więc i w
(a więc i w  )
do rozwiązania uogólnionego
)
do rozwiązania uogólnionego 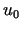 równania
równania 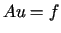 oraz
oraz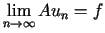 w
w  .
.
U w a g a 1 (porównanie z metodą Ritza)
Niech 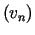 oznacza ciąg Ritza, zaś
oznacza ciąg Ritza, zaś 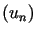 ciąg otrzymany metodą najmniejszych kwadratów. Wówczas, ponieważ
ciąg otrzymany metodą najmniejszych kwadratów. Wówczas, ponieważ 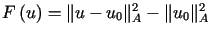 ,
więc z konstrukcji ciągu Ritza wynika, że
,
więc z konstrukcji ciągu Ritza wynika, że
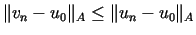 , , |
(14.22) |
co oznacza, że ciąg Ritza jest ,,szybciej'' zbieżny. Z drugiej strony metoda
najmniejszych kwadratów pozwala prosto oszacować popełniony błąd, bowiem
na mocy nierówności (14.9) prawdziwe jest
oszacowanie 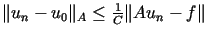 .
.
U w a g a 2
W przypadku, gdy wiadomo, że 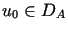 można rozważyć funkcjonał
można rozważyć funkcjonał
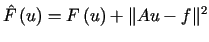 i zastosować do niego metodę Ritza. Wówczas ciąg minimalizujący
i zastosować do niego metodę Ritza. Wówczas ciąg minimalizujący 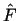 spełnia dodatkowo warunek
spełnia dodatkowo warunek 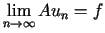 w
w  .
Metoda ta nosi nazwę metody Couranta.
.
Metoda ta nosi nazwę metody Couranta.
U w a g a 3
Do formalnego zastosowania metody najmniejszych kwadratów nie jest konieczne,
żeby operator 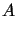 był dodatnio określony. Problem jednoznaczności wyznaczenia współczynników
był dodatnio określony. Problem jednoznaczności wyznaczenia współczynników 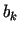 i zbieżności ciągu
i zbieżności ciągu 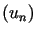 ma odpowiedź pozytywną przy następujących założeniach:
ma odpowiedź pozytywną przy następujących założeniach:
-
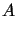 - liniowy,
- liniowy, 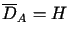 ;
;
-
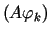 jest bazą w
jest bazą w  ;
;
-
Równanie
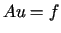 ma rozwiązanie
ma rozwiązanie 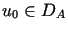 ;
;
-
Istnieje stała
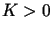 taka, że dla każdego
taka, że dla każdego 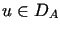 zachodzi nierówność
zachodzi nierówność 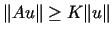 .
.




Next:Metoda
gradientówUp:Wstęp
do metod przybliżonychPrevious:Metoda
GalerkinaSpis
rzeczy
Administrator 2003-04-24
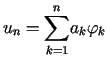
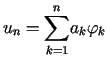
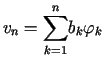 .
.
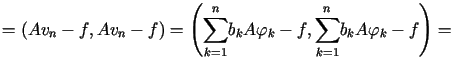
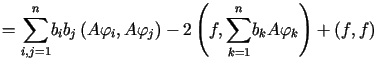 .
.![]() dla
dla ![]() co można zapisać w postaci układu równań
co można zapisać w postaci układu równań
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2934 \left(......varphi _{n}\right) b_{n} & =\left( f,A\varphi_{n}\right) \end{array} \right.%%$](img2100.gif)
![]() będzie operatorem liniowym dodatnio określonym na
będzie operatorem liniowym dodatnio określonym na ![]() ,
,![]() gęsty w
gęsty w ![]() ,
, ![]() ,
, ![]() - ośrodkowa przestrzeń Hilberta. Niech
- ośrodkowa przestrzeń Hilberta. Niech ![]() będzie
będzie ![]() bazą
w
bazą
w ![]() (tzn.
(tzn. ![]() jest bazą w
jest bazą w ![]() )
oraz
)
oraz ![]() dla
dla ![]() .
Wówczas ciąg
.
Wówczas ciąg ![]() postaci
postaci
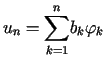
![]() oznacza ciąg Ritza, zaś
oznacza ciąg Ritza, zaś ![]() ciąg otrzymany metodą najmniejszych kwadratów. Wówczas, ponieważ
ciąg otrzymany metodą najmniejszych kwadratów. Wówczas, ponieważ ![]() ,
więc z konstrukcji ciągu Ritza wynika, że
,
więc z konstrukcji ciągu Ritza wynika, że
![]() można rozważyć funkcjonał
można rozważyć funkcjonał
![]() był dodatnio określony. Problem jednoznaczności wyznaczenia współczynników
był dodatnio określony. Problem jednoznaczności wyznaczenia współczynników ![]() i zbieżności ciągu
i zbieżności ciągu ![]() ma odpowiedź pozytywną przy następujących założeniach:
ma odpowiedź pozytywną przy następujących założeniach: