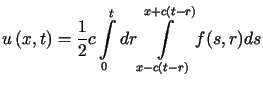 . . |
(2.6) |
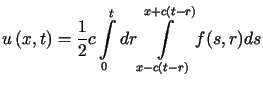 . . |
(2.6) |
Poprzez bezpośrednie różniczkowanie łatwo sprawdzić, że funkcja ![]() spełnia równanie (2.1) oraz, że
spełnia równanie (2.1) oraz, że ![]() .
Ponieważ
.
Ponieważ
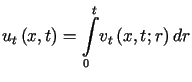 ,
gdzie
,
gdzie 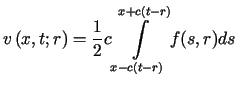 ,
,Wynika stąd, że rozwiązanie zagadnienia początkowego (2.1)-(2.2)
można zapisać jako sumę rozwiązania danego wzorem d'Alemberta (2.5)
i funkcji ![]() określonej wzorem (2.6).
określonej wzorem (2.6).
W ten sposób otrzymujemy wzór d'Alemberta dla równania niejednorodnego
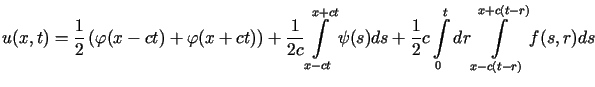 |
(2.7) |