



Next:Struna
jednostronnie ograniczonaUp:Struna
nieograniczonaPrevious:Zagadnienie
Cauchy'ego dla równaniaSpis
rzeczy
Stabilność rozwiązania
Niech 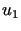 i
i 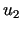 będą rozwiązaniami zagadnienia (2.1)-(2.2)
odpowiednio dla par funkcji danych
będą rozwiązaniami zagadnienia (2.1)-(2.2)
odpowiednio dla par funkcji danych 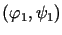 i
i 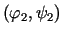 .
Załóżmy, że dla wszystkich
.
Załóżmy, że dla wszystkich 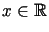 zachodzą nierówności
zachodzą nierówności
Na mocy wzoru d'Alemberta (2.7) można
napisać, że
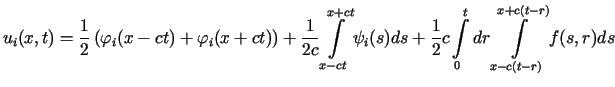 dla
dla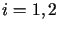 .
. Jeśli rozważać będziemy ewolucję kształtu struny w przedziale czasowym
Jeśli rozważać będziemy ewolucję kształtu struny w przedziale czasowym ![$ \left[ 0,T_{0}\right] $](img306.gif) ,
to korzystając z (2.8) różnicę pomiędzy rozwiązaniami
,
to korzystając z (2.8) różnicę pomiędzy rozwiązaniami 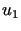 i
i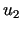 możemy oszacować następująco
możemy oszacować następująco
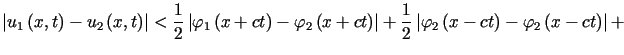
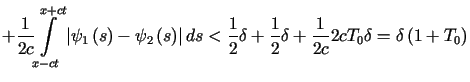 .
. |
(2.9) |
Ostatnia nierówność oznacza, że powyższe zagadnienie jest stabilne.
O ile bowiem warunki początkowe zadania nie różnią się o więcej niż o 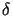 ,
to również rozwiązania w dowolnym zadanym lecz ustalonym przedziale czasowym
nie różnią się o więcej niż o liczbę
,
to również rozwiązania w dowolnym zadanym lecz ustalonym przedziale czasowym
nie różnią się o więcej niż o liczbę 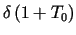 .
Oznacza to ciagłą zależność rozwiązania od warunków początkowych, ponieważ
.
Oznacza to ciagłą zależność rozwiązania od warunków początkowych, ponieważ 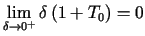 .
.
W takim razie zagadnienie Cauchy'ego dla równania struny jest poprawnie
postawione.




Next:Struna
jednostronnie ograniczonaUp:Struna
nieograniczonaPrevious:Zagadnienie
Cauchy'ego dla równaniaSpis
rzeczy
Administrator 2003-01-24
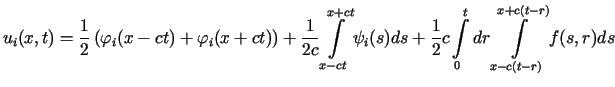 dla
dla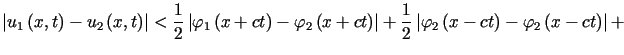
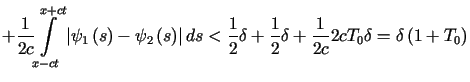 .
.![]() ,
to również rozwiązania w dowolnym zadanym lecz ustalonym przedziale czasowym
nie różnią się o więcej niż o liczbę
,
to również rozwiązania w dowolnym zadanym lecz ustalonym przedziale czasowym
nie różnią się o więcej niż o liczbę ![]() .
Oznacza to ciagłą zależność rozwiązania od warunków początkowych, ponieważ
.
Oznacza to ciagłą zależność rozwiązania od warunków początkowych, ponieważ ![]() .
.