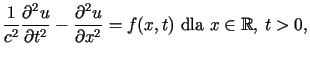 |
(2.1) |
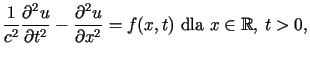 |
(2.1) |
gdzie ![]() oznacza wychylenie struny z położenia równowagi w punkcie
oznacza wychylenie struny z położenia równowagi w punkcie ![]() ,
w chwili czasu
,
w chwili czasu![]() Funkcja
Funkcja ![]() przedstawia gęstość siły zewnętrznej, działającej na strunę. Postać ta
jest równoważna postaci (1.2). Dla powyższego
równania rozważać będziemy zagadnienie początkowe w przypadku jednorodnym
(drgania swobodne) i niejednorodnym (drgania wymuszone).
przedstawia gęstość siły zewnętrznej, działającej na strunę. Postać ta
jest równoważna postaci (1.2). Dla powyższego
równania rozważać będziemy zagadnienie początkowe w przypadku jednorodnym
(drgania swobodne) i niejednorodnym (drgania wymuszone).
Załóżmy, że mamy do czynienia z drganiami swobodnymi, tzn.![]() .
Rozważamy następujące zagadnienie.
.
Rozważamy następujące zagadnienie.
Wyznaczyć funkcję ![]() spełniającą równanie (2.1) i warunki początkowe
spełniającą równanie (2.1) i warunki początkowe
| (2.2) |
Zakładamy, że ![]() jest klasy
jest klasy ![]() ,
zaś
,
zaś ![]() jest klasy
jest klasy![]() .
.
Zagadnienie (2.1)-(2.2)
rozwiążemy stosując metodę d'Alemberta.
Stosując w równaniu (2.1) zamianę zmiennych ![]() ,
,![]() sprowadzamy je do postaci kanonicznej
sprowadzamy je do postaci kanonicznej
| (2.3) |
Funkcje ![]() i
i ![]() należy dobrać w ten sposób, aby spełnione były warunki początkowe (2.2).
Warunki (2.2) prowadzą do układu równań funkcyjnych
należy dobrać w ten sposób, aby spełnione były warunki początkowe (2.2).
Warunki (2.2) prowadzą do układu równań funkcyjnych
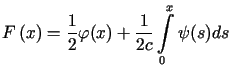 i
i 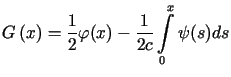 . . |
(2.4) |
Podstawiając wzory (2.4) do (2.3) otrzymujemy tzw. wzór d'Alemberta dla struny swobodnej
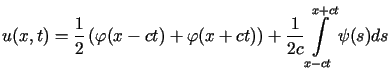 . . |
(2.5) |
Z powyższych wzorów wynika, że zaburzenie kształtu struny spowodowane
przez przyjęte warunki początkowe rozchodzi się ze skończoną prędkością
wzdłuż osi ![]() .
Funkcja
.
Funkcja![]() występująca we wzorze (2.3) przedstawia falę
rozchodzącą się z prędkością
występująca we wzorze (2.3) przedstawia falę
rozchodzącą się z prędkością ![]() w dodatnim kierunku osi
w dodatnim kierunku osi ![]() zaś funkcja
zaś funkcja ![]() - falę rozchodzącą się z prędkością
- falę rozchodzącą się z prędkością ![]() w ujemnym kierunku osi
w ujemnym kierunku osi ![]() Rozwiązanie
Rozwiązanie![]() jest sumą tych dwóch fal.
jest sumą tych dwóch fal.
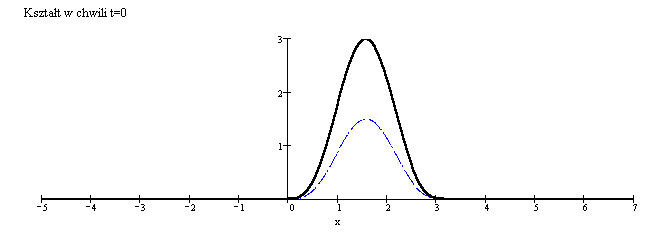
Rozwiązać zagadnienie (2.1)-(2.2)
przyjmując ![]() oraz
oraz
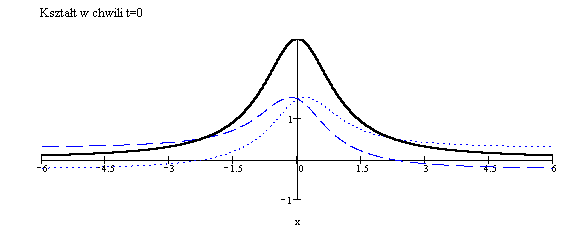
P r z y k ł a d 2
Rozwiązać zagadnienie (2.1)-(2.2)
przyjmując ![]() ,
,![]() oraz
oraz