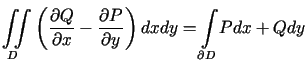 |
(6.3) |
Rozważmy znany wzór Greena w postaci
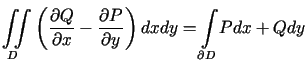 |
(6.3) |
dla funkcji ![]() i
i ![]() klasy
klasy ![]() .
Podstawiając
.
Podstawiając ![]() ,
, ![]() otrzymujemy
otrzymujemy
![$\displaystyle <tex2html_comment_mark>805 {\displaystyle\iint\limits_{D}} \left(......_{\partial D}} \left[ u\cos\left( x,n\right) +v\cos\left( y,n\right) \right] ds$](img832.gif) , , |
(6.4) |
gdzie ![]() oznacza wektor normalny zewnętrzny do
oznacza wektor normalny zewnętrzny do ![]() .
.
Zastępując we wzorze (6.4) ![]() przez
przez ![]() i
i ![]() przez
przez ![]() ,
dostajemy tzw.
pierwszą tożsamość Greena
,
dostajemy tzw.
pierwszą tożsamość Greena
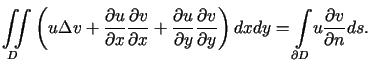 |
(6.5) |
Zamieniając rolami ![]() i
i ![]() we wzorze (6.5) i odejmując otrzymany wzór
od (6.5) otrzymujemy tzw. drugą tożsamość
Greena
we wzorze (6.5) i odejmując otrzymany wzór
od (6.5) otrzymujemy tzw. drugą tożsamość
Greena
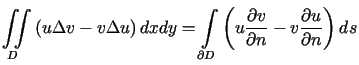 . . |
(6.6) |
Niech teraz ![]() będzie ustalonym punktem, zaś
będzie ustalonym punktem, zaś ![]() zmiennym. Wprowadzając funkcję
zmiennym. Wprowadzając funkcję
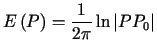 |
(6.7) |
można pokazać, że zachodzi równość
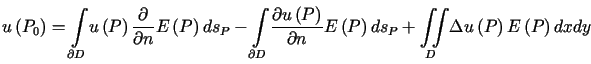 . . |
(6.8) |
Równość (6.8) zwana jest trzecią tożsamością
Greena lub wzorem podstawowym teorii funkcji harmonicznych.
Funkcję![]() określoną wzorem (6.7) nazywamy rozwiązaniem
podstawowym równania Laplace'a.
określoną wzorem (6.7) nazywamy rozwiązaniem
podstawowym równania Laplace'a.
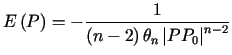 dla
dla |
(6.9) |
gdzie ![]() ,
, ![]() ,
, ![]() oznacza miarę powierzchni kuli jednostkowej w
oznacza miarę powierzchni kuli jednostkowej w ![]()
![$\displaystyle \theta_{n}=\left\{ \begin{array}[c]{ll}<tex2html_comment_mark>849......t{dla }n\text{ nieparzystych,}<tex2html_comment_mark>850 \end{array} \right.%%$](img849.gif) |
(6.10) |
można wyprowadzić wzór podstawowy dla ![]() ,
postaci
,
postaci
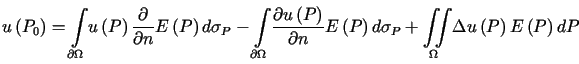 . . |
(6.11) |
Jest to odpowiednik wzoru (6.8).