Spis rzeczy

Funkcje harmoniczne

Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję.
 

D e f i n i c j a

Funkcję $u\left( x_{1},x_{2},\ldots,x_{n}\right)$ nazywamy harmoniczną w obszarze $D\subset\mathbb{R}^{n}$ wtedy i tylko wtedy, gdy jest klasy $C^{2}$ oraz

$$\Delta u=0 %%$$ (6.1)

gdzie $\Delta u=u_{x_{1}x_{1}}+\ldots+u_{x_{n}x_{n}}$ jest operatorem Laplace'a.

W przypadku $n=2$ można wykazać, że lokalnie każda funkcja harmoniczna jest częścią rzeczywistą pewnej funkcji holomorficznej.
 

T w i e r d z e n i e

Jeżeli funkcja $u\left( x,y\right)$ jest harmoniczna w kole$K\subset\mathbb{R}^{2}$, to istnieje funkcja harmoniczna $v\left(x,y\right)$ określona wzorem

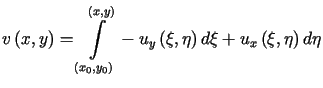$$v\left( x,y\right) =<tex2html_comment_mark>787 {\displaystyle\int......ight) }} -u_{y}\left( \xi,\eta\right) d\xi+u_{x}\left( \xi,\eta\right) d\eta%%$$ (6.2)

taka, że $f=u+iv$ jest funkcją holomorficzną.

Dowód polega na sprawdzeniu, że spełnione są tzw. równania Cauchy'ego-Riemanna gwarantujące holomorficzność funkcji $f$. Równania te są postaci: $u_{x}=v_{y}$, $u_{y}=-v_{x}$.