Spis rzeczy

Własności funkcji harmonicznych

Podamy teraz podstawowe własności funkcji harmonicznych. Rozważymy najpierw przypadek $n=2$.
 

T w i e r d z e n i e  1

Jeśli funkcja $u$ jest harmoniczna w pewnym ograniczonym obszarze$D_{1}\supset\overline{D}$, to

$$%%{\displaystyle\int\limits_{\partial D}}\frac{\partial u}{\partial n}ds=0$$.$$%%$$ Dowód wynika z pierwszej tożsamości Greena (6.5), w którym należy podstawić w miejsce funkcji $u$ funkcję stałą równą $1$, a w miejsce funkcji $v$ funkcję $u$.
 
 

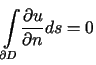T w i e r d z e n i e  2

Jeśli funkcja $u$ jest klasy $C^{2}$ w obszarze ograniczonym $D$ oraz

$$%%{\displaystyle\int\limits_{\Gamma}}\frac{\partial u}{\partial n}ds=0$$,$$%%$$ dla każdego gładkiego i zamkniętego łuku $\Gamma$ ograniczającego obszar $D_{0}\subset D$, to $u$ jest harmoniczna w $D$.
 

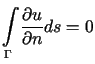D o w ó d

Stosując wzór (6.5) dla $u=1$ i $v=u$ otrzymujemy, że

$$%%{\displaystyle\iint\limits_{D_{0}}}\Delta udxdy=%%{\displaystyle\int\limits_{\Gamma}}\frac{\partial u}{\partial n}ds=0$$ dla dowolnego $D_{0}\subset D$, zatem $\Delta u=0$ dla $\left( x,y\right)\in D_{0}$.
 

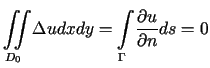
T w i e r d z e n i e  3

Niech $u$ będzie funkcją harmoniczną w ograniczonym obszarze $D$ i klasy $C^{1}$ w $\overline{D}$. Jeśli $u_{\vert\partial D}=0$, to $u\equiv0$ w$D$. Jeśli $\frac{\partial u}{\partial n}_{\vert\partial D}=0$, to $u\equivconst$ w $D.\bigskip$

D o w ó d

Podstawiając $u=v$ w pierwszej tożsamości Greena (6.5) otrzymujemy

$$%%{\displaystyle\iint\limits_{D}}\left[ \left( \frac{\partial u......y=%%{\displaystyle\int\limits_{\partial D}}u\frac{\partial u}{\partial n}ds=0$$,$$%%$$ skąd wynika natychmiast, że $\frac{\partial u}{\partial x}\equiv\frac{\partial u}{\partial y}\equiv0$ w $D.$ W takim razie $u$ jest stała, lub stała i równa zero, w zależności od przyjętego założenia.
 

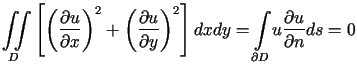Załóżmy teraz, że $n\geq2$. Można wykazać prawdziwość następującego twierdzenia.

T w i e r d z e n i e  4 (tw. Gaussa o wartości średniej funkcji harmonicznej)

Jeśli $u$ jest funkcją harmoniczną w kuli $K\left( a,R\right)$, klasy $C^{2}$ w $\overline{K}\left( a,R\right)$, to w środku tej kuli przyjmuje ona wartość równą średniej wartości na powierzchni kuli. Zależność tę opisuje wzór

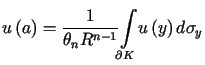$$u\left( a\right) =\frac{1}{\theta_{n}R^{n-1}}<tex2html_comment_mark>904 {\displaystyle\int\limits_{\partial K}} u\left( y\right) d\sigma_{y} %%$$ (6.12)

gdzie $\theta_{n}$ oznacza miarę powierzchni kuli jednostkowej w$\mathbb{R}^{n}$ określoną wzorem (6.10).
 

W przypadku $n=2$ dla $a=\left( x_{0},y_{0}\right)$ wzór (6.12) przybiera postać

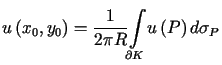$$u\left( x_{0},y_{0}\right) =\frac{1}{2\pi R}<tex2html_comment_mark>913 {\displaystyle\int\limits_{\partial K}} u\left( P\right) d\sigma_{P} %%$$ (6.13)

zaś dla $n=3$ i $a=\left( x_{0},y_{0},z_{0}\right)$ mamy

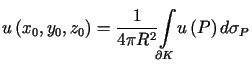$$u\left( x_{0},y_{0},z_{0}\right) =\frac{1}{4\pi R^{2}}<tex2html_c......t_mark>918 {\displaystyle\int\limits_{\partial K}} u\left( P\right) d\sigma_{P} %%$$ (6.14)

U w a g a

W przypadku $n=2$ łatwo pokazać, że

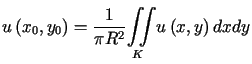$$u\left( x_{0},y_{0}\right) =\frac{1}{\pi R^{2}}<tex2html_comment_mark>923 {\displaystyle\iint\limits_{K}} u\left( x,y\right) dxdy %%$$ (6.15)

a więc wartość funkcji harmonicznej w środku koła równa jest średniej wartości tej funkcji w całym kole.
 

Ważnym wnioskiem wynikającym z twierdzenia Gaussa o wartości średniej funkcji harmonicznej, jest tzw. zasada maksimum dla funkcji harmonicznych.
 

T w i e r d z e n i e  5 (zasada maksimum)

Niech $u$ będzie funkcją harmoniczną w obszarze $D$ (ograniczonym lub nie) przyjmującą wartości rzeczywiste. Jeżeli $u$ nie jest tożsamościowo równa stałej, to nie może ona przyjmować w żadnym punkcie obszaru $D$ swego kresu górnego ani dolnego.
 

Bezpośrednio z zasady maksimum można wyprowadzić dwa ważne wnioski.
 

W n i o s e k  1

Jeżeli $u_{1}$, $u_{2}$ są harmoniczne w $D$, ciągłe w$\overline{D}$ oraz

$$u_{1\vert\partial D}\leq u_{2\vert\partial D}$$,$$%%$$ to $u_{1}\leq u_{2}$ w $D$.

Dowód wynika z zastosowania zasady maksimum do funkcji harmonicznej$u_{2}-u_{1}$.

W n i o s e k  2

Jeżeli $u_{1}$, $u_{2}$ są harmoniczne w $D$, ciągłe w$\overline{D}$ oraz

$$\left\vert u_{1}\right\vert \leq u_{2}$$ na $$\partial D$$,$$%%$$ to $\left\vert u_{1}\right\vert \leq u_{2}$ w $D$.

Dowód wynika z zastosowania wniosku $1$ do par funkcji $-u_{2}$, $u_{1}$ oraz $u_{1}$, $u_{2}$.
 

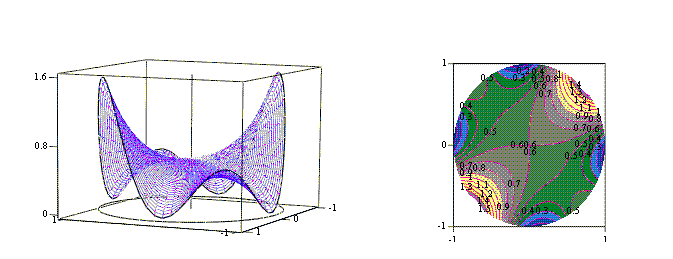
Poniższy rysunek ilustruje pewne charakterystyczne cechy funkcji harmonicznych. Przedstawia on powierzchnię opisaną wzorem

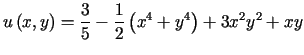$$u\left( x,y\right) =\frac{3}{5}-\frac{1}{2}\left( x^{4}+y^{4}\right)+3x^{2}y^{2}+xy$$,$$%%$$ która jest przykładem funkcji harmonicznej dwóch zmiennych. Powierzchnia jest widoczna dla $\left( x,y\right)$ należących do koła jednostkowego $x^{2}+y^{2}\leq1$. Widoczny jest także plan warstwicowy.