



Next:Zagadnienia
brzegowe dla równań eliptycznychUp:Funkcje
harmonicznePrevious:Własności
funkcji harmonicznychSpis
rzeczy
Zadania
W zadaniach 1 -11 należy znaleźć funkcję holomorficzną 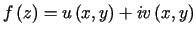 wiedząc, że:
wiedząc, że:
-
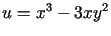
-
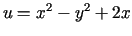
-
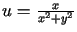
-
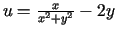
-
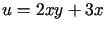
-
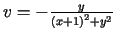
-
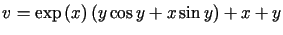
-
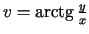 ,
, 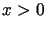
-
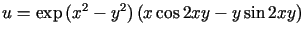
-
![$ u=\exp\left( x\right) \left[ \left( x^{2}-y^{2}+1\right) \cosy-2xy\sin y\right] $](img898.gif)
-
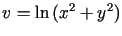
-
Znaleźć punkty, w których funkcja
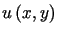 osiąga swój kres górny i dolny w zbiorze
osiąga swój kres górny i dolny w zbiorze 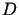 ,
jeżeli: a)
,
jeżeli: a) 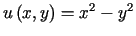 ,
, 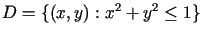 ,
b)
,
b) 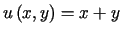 ,
, 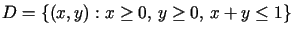
-
Udowodnić wzór (6.15) wykorzystując twierdzenie
Gaussa o wartości średniej w przypadku
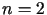 .
.
-
Udowodnić, że funkcja harmoniczna o wartościach rzeczywistych, nie będąca
stałą, nie może posiadać ekstremów lokalnych w żadnym punkcie obszaru,
w którym jest określona.
-
Załóżmy, że funkcja
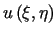 jest harmoniczna, a funkcja
jest harmoniczna, a funkcja 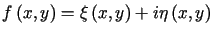 jest holomorficzna, tzn. spełniony jest układ równań Cauchy'ego-Riemanna
jest holomorficzna, tzn. spełniony jest układ równań Cauchy'ego-Riemanna 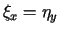 ,
, 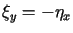 .
Pokazać, że złożenie
.
Pokazać, że złożenie 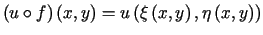 jest funkcją harmoniczną (zakładamy wykonalność złożenia).
jest funkcją harmoniczną (zakładamy wykonalność złożenia).
Administrator 2003-02-13
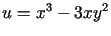
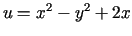
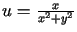
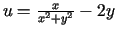
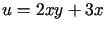
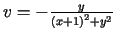
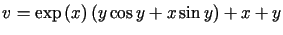
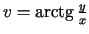 ,
, 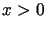
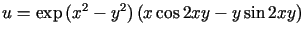
![$ u=\exp\left( x\right) \left[ \left( x^{2}-y^{2}+1\right) \cosy-2xy\sin y\right] $](img898.gif)
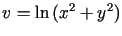
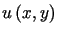 osiąga swój kres górny i dolny w zbiorze
osiąga swój kres górny i dolny w zbiorze 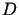 ,
jeżeli: a)
,
jeżeli: a) 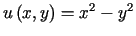 ,
, 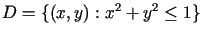 ,
b)
,
b) 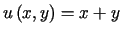 ,
, 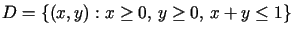
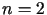 .
.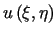 jest harmoniczna, a funkcja
jest harmoniczna, a funkcja 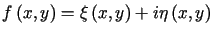 jest holomorficzna, tzn. spełniony jest układ równań Cauchy'ego-Riemanna
jest holomorficzna, tzn. spełniony jest układ równań Cauchy'ego-Riemanna 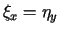 ,
, 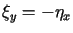 .
Pokazać, że złożenie
.
Pokazać, że złożenie 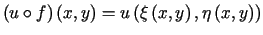 jest funkcją harmoniczną (zakładamy wykonalność złożenia).
jest funkcją harmoniczną (zakładamy wykonalność złożenia).