



Next:Metoda
funkcji GreenaUp:indexPrevious:ZadaniaSpis
rzeczy
Zagadnienia brzegowe dla równań
eliptycznych
Rozważmy płaski obszar 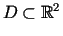 ograniczony krzywą
ograniczony krzywą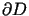 .
Dla równania Laplace'a (Poissona) stawia się trzy podstawowe zagadnienia
brzegowe.
.
Dla równania Laplace'a (Poissona) stawia się trzy podstawowe zagadnienia
brzegowe.
-
Zagadnienie Dirichleta (tzw. zagadnienie brzegowe pierwszego
rodzaju)
Znaleźć funkcję 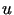 spełniającą warunki
spełniającą warunki
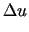 |
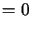 (lub
(lub 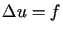 ),
dla ),
dla 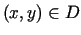 , , |
(7.1) |
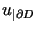 |
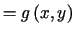 , , |
(7.2) |
gdzie 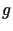 jest funkcją daną określoną na
jest funkcją daną określoną na 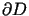 .
Warunek (7.2) rozumiany jest w sensie przejścia
granicznego jako
.
Warunek (7.2) rozumiany jest w sensie przejścia
granicznego jako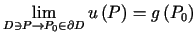 .
.
-
Zagadnienie Neumanna (tzw. zagadnienie brzegowe drugiego rodzaju)
Znaleźć funkcję 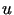 spełniającą warunki
spełniającą warunki
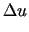 |
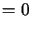 (lub
(lub 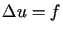 ),
dla ),
dla 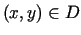 , , |
(7.3) |
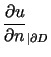 |
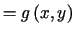 , ,  |
(7.4) |
gdzie 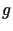 jest funkcją daną określoną na
jest funkcją daną określoną na 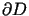 ,
, 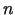 jest wektorem normalnym zewnętrznym. Warunek (7.4)
również należy rozumieć w sensie przejścia do granicy od wnętrza obszaru.
jest wektorem normalnym zewnętrznym. Warunek (7.4)
również należy rozumieć w sensie przejścia do granicy od wnętrza obszaru.
-
Zagadnienie Robina (tzw. zagadnienie brzegowe trzeciego rodzaju)
Znaleźć funkcję 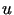 spełniającą warunki
spełniającą warunki
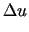 |
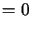 (lub
(lub 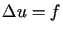 ),
dla ),
dla 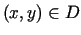 , , |
(7.5) |
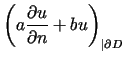 |
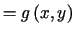 , ,  |
(7.6) |
gdzie 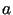 ,
, 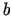 ,
, 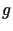 są danymi funkcjami określonymi na
są danymi funkcjami określonymi na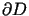 ,
,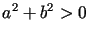 ,
, 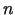 jest wektorem normalnym zewnętrznym. Warunek (7.6)
również należy rozumieć w sensie przejścia granicznego.
jest wektorem normalnym zewnętrznym. Warunek (7.6)
również należy rozumieć w sensie przejścia granicznego.
Postawione zagadnienia są tzw. zagadnieniami wewnętrznymi. Stawia
się ponadto zagadnienia zewnętrzne dla obszarów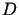 nieograniczonych, zewnętrznych względem danych krzywych początkowych.
nieograniczonych, zewnętrznych względem danych krzywych początkowych.
W tym przypadku należy dodatkowo przyjąć, że poszukiwana funkcja spełnia
pewien warunek dotyczący zachowania się jej dla punktów odległych od początku
układu, tzw. ,,warunek w nieskończoności''.
Dla równania Laplace'a nie stawia się zagadnienia Cauchy'ego, poza jednym
przypadkiem, gdy poszukuje się lokalnie rozwiązania w klasie funkcji analitycznych
przy analitycznych danych początkowych. Powodem tego jest fakt, że zagadnienie
Cauchy'ego dla równania Laplace'a nie jest poprawnie postawione (patrz
przykład z wykładu 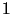 ).
).
Subsections




Next:Metoda
funkcji GreenaUp:indexPrevious:ZadaniaSpis
rzeczy
Administrator 2003-02-19
![]() jest funkcją daną określoną na
jest funkcją daną określoną na ![]() .
Warunek (7.2) rozumiany jest w sensie przejścia
granicznego jako
.
Warunek (7.2) rozumiany jest w sensie przejścia
granicznego jako![]() .
.
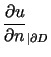
![]() jest funkcją daną określoną na
jest funkcją daną określoną na ![]() ,
, ![]() jest wektorem normalnym zewnętrznym. Warunek (7.4)
również należy rozumieć w sensie przejścia do granicy od wnętrza obszaru.
jest wektorem normalnym zewnętrznym. Warunek (7.4)
również należy rozumieć w sensie przejścia do granicy od wnętrza obszaru.
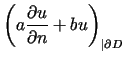
![]() ,
, ![]() ,
, ![]() są danymi funkcjami określonymi na
są danymi funkcjami określonymi na![]() ,
,![]() ,
, ![]() jest wektorem normalnym zewnętrznym. Warunek (7.6)
również należy rozumieć w sensie przejścia granicznego.
jest wektorem normalnym zewnętrznym. Warunek (7.6)
również należy rozumieć w sensie przejścia granicznego.