



Next: Zadania
Up: Zagadnienia brzegowe dla równań
Previous: Jednoznaczność zagadnienia Dirichleta i
Spis rzeczy
Załóżmy, że 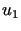 i
i 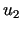 są rozwiązaniami
zagadnienia Dirichleta dla równania Poissona
są rozwiązaniami
zagadnienia Dirichleta dla równania Poissona
z warunkami brzegowymi
W takim razie funkcja
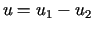 jest rozwiązaniem zagadnienia
Dirichleta dla równania Laplace'a
Przypuśćmy, że dla każdego
jest rozwiązaniem zagadnienia
Dirichleta dla równania Laplace'a
Przypuśćmy, że dla każdego
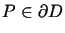 zachodzi
nierówność
zachodzi
nierówność
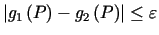
.

Ponieważ funkcja stała równa
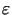 , jest funkcją
harmoniczną, więc na mocy wniosku
, jest funkcją
harmoniczną, więc na mocy wniosku 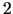 z zasady maksimum dla funkcji
harmonicznych (patrz poprzedni wykład), zachodzi nierówność
dla dowolnych punktów
z zasady maksimum dla funkcji
harmonicznych (patrz poprzedni wykład), zachodzi nierówność
dla dowolnych punktów
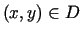 , co dowodzi
stabilności rozwiązania.
, co dowodzi
stabilności rozwiązania.
Administrator
2003-02-19
![]() i
i ![]() są rozwiązaniami
zagadnienia Dirichleta dla równania Poissona
są rozwiązaniami
zagadnienia Dirichleta dla równania Poissona