



Next:Stabilność
rozwiązania zagadnienia DirichletaUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
odwzorowań konforemnychSpis
rzeczy
Jednoznaczność zagadnienia Dirichleta
i Neumanna
Niech 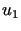 i
i 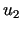 będą dwoma rozwiązaniami zagadnienia Dirichleta dla równania Laplace'a
(Poissona). Wówczas różnica
będą dwoma rozwiązaniami zagadnienia Dirichleta dla równania Laplace'a
(Poissona). Wówczas różnica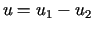 jest rozwiązaniem zagadnienia
jest rozwiązaniem zagadnienia
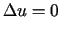 ,
dla
,
dla 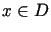 ,
, 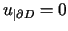 .
. Z własności
Z własności 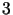 funkcji harmonicznych wynika, że
funkcji harmonicznych wynika, że 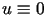 ,
zatem
,
zatem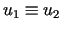 w
w 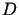 .
.
W przypadku zagadnienia Neumanna różnica 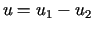 dwóch rozwiązań tego zagadnienia jest rozwiązaniem problemu
dwóch rozwiązań tego zagadnienia jest rozwiązaniem problemu
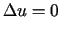 ,
dla
,
dla 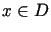 ,
, 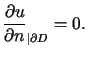 Na mocy własności
Na mocy własności 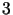 funkcji harmonicznych wnioskujemy, że
funkcji harmonicznych wnioskujemy, że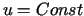 .
O ile więc nie przyjmiemy jakiegoś dodatkowego założenia, to nie możemy
twierdzić, że rozwiązanie zagadnienia Neumanna, o ile istnieje, jest jedyne.
Zwykle takim dodatkowym założeniem gwarantującym jednoznaczność rozwiązania
jest podanie wartości
.
O ile więc nie przyjmiemy jakiegoś dodatkowego założenia, to nie możemy
twierdzić, że rozwiązanie zagadnienia Neumanna, o ile istnieje, jest jedyne.
Zwykle takim dodatkowym założeniem gwarantującym jednoznaczność rozwiązania
jest podanie wartości 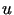 w jakimś punkcie obszaru
w jakimś punkcie obszaru 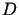 .
.
U w a g a
Z pierwszej tożsamości Greena (6.5) dla 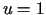 ,
, 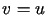 wynika, że
wynika, że
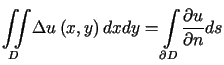 .
. Oznacza to, że w zagadnieniu Neumanna nie można zadać wartości pochodnej
Oznacza to, że w zagadnieniu Neumanna nie można zadać wartości pochodnej 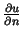 na brzegu
na brzegu  w sposób dowolny. W szczególności funkcje dane muszą spełniać warunek
w sposób dowolny. W szczególności funkcje dane muszą spełniać warunek
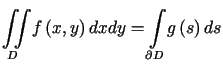 . . |
(7.24) |
Jest to warunek konieczny rozwiązalności tego zagadnienia.




Next:Stabilność
rozwiązania zagadnienia DirichletaUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
odwzorowań konforemnychSpis
rzeczy
Administrator 2003-02-19
![]() dwóch rozwiązań tego zagadnienia jest rozwiązaniem problemu
dwóch rozwiązań tego zagadnienia jest rozwiązaniem problemu
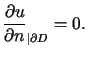
![]() ,
, ![]() wynika, że
wynika, że
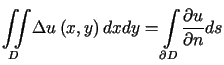 .
.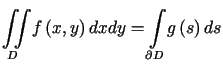 .
.