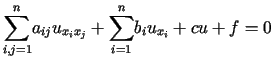 ,
( ,
( |
(1.12) |
gdzie współczynniki ![]() ,
, ![]() ,
, ![]() ,
, ![]() zależą od
zależą od ![]() .
.
Z równaniem tym związana jest forma kwadratowa zmiennych ![]()
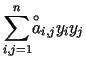 , , |
(1.13) |
gdzie ![]() oznacza
wartość współczynnika
oznacza
wartość współczynnika![]() w pewnym punkcie
w pewnym punkcie ![]() .
Macierz
.
Macierz ![]() formy (1.13) możemy sprowadzić do postaci
kanonicznej, w której na przekątnej mogą znajdować się tylko liczby
formy (1.13) możemy sprowadzić do postaci
kanonicznej, w której na przekątnej mogą znajdować się tylko liczby ![]() ,
, ![]() lub 0, zaś wszystkie elementy poza przekątną są równe zero. Zgodnie z twierdzeniem
o bezwładności form kwadratowych liczba współczynników dodatnich, ujemnych
i równych zeru jest niezmiennicza względem przekształcenia liniowego sprowadzającego
formę (1.13) do postaci kanonicznej (zauważmy,
że postać kanoniczna formy kwadratowej nie jest jednoznacznie wyznaczona).
lub 0, zaś wszystkie elementy poza przekątną są równe zero. Zgodnie z twierdzeniem
o bezwładności form kwadratowych liczba współczynników dodatnich, ujemnych
i równych zeru jest niezmiennicza względem przekształcenia liniowego sprowadzającego
formę (1.13) do postaci kanonicznej (zauważmy,
że postać kanoniczna formy kwadratowej nie jest jednoznacznie wyznaczona).
Niech ![]() oznaczają współczynniki formy (1.13) w postaci
kanonicznej. W zależności od zachowania się współczynników
oznaczają współczynniki formy (1.13) w postaci
kanonicznej. W zależności od zachowania się współczynników ![]() wprowadzamy definicję typu równania (1.12).
wprowadzamy definicję typu równania (1.12).
D e f i n i c j a
Mówimy, że równanie (1.12) jest w punkcie ![]() typu
typu
W zależności od typu równania w punkcie ![]() można je sprowadzić w tym punkcie do jednej z następujących postaci kanonicznych:
można je sprowadzić w tym punkcie do jednej z następujących postaci kanonicznych:
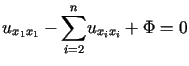 ;
(typ hiperboliczny)
;
(typ hiperboliczny)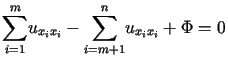 (
(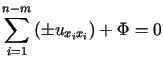 (
(