Przestrzenią funkcji szybkomalejących nazywamy zbiór funkcji
klasy![]() spełniających dla
spełniających dla ![]() ,
dowolnych n, k naturalnych, nierówności
,
dowolnych n, k naturalnych, nierówności
| (9.7) |
dla pewnych stałych ![]() (zależnych tylko od n i k). Przestrzeń funkcji szybkomalejących oznaczamy
symbolem
(zależnych tylko od n i k). Przestrzeń funkcji szybkomalejących oznaczamy
symbolem ![]() .
.
Powyższy warunek oznacza, że dowolna pochodna funkcji ![]() dąży do zera w nieskończoności szybciej niż dowolna potęga
dąży do zera w nieskończoności szybciej niż dowolna potęga ![]() .
.
U w a g a
Zachodzi oczywista inkluzja ![]() ,
bowiem każda funkcja o nośniku zwartym jest szybkomalejąca. Co więcej,
rozważając przykład funkcji
,
bowiem każda funkcja o nośniku zwartym jest szybkomalejąca. Co więcej,
rozważając przykład funkcji ![]() łatwo zauważyć, że
łatwo zauważyć, że ![]() ,
zatem
,
zatem ![]() .
.
D e f i n i c j a
Mówimy, że ciąg funkcji ![]() zbiega do
zbiega do ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy ![]()
![]()
![]() (zb. jednostajna)
(zb. jednostajna)
D e f i n i c j a
Dystrybucją wolnorosnącą (temperowaną) nazywamy funkcjonał
liniowy i ciągły na przestrzeni ![]() .
Zbiór dytrybucji wolnorosnących oznaczamy
.
Zbiór dytrybucji wolnorosnących oznaczamy ![]() .
.
U w a g a
Oczywiście jeżeli ![]() ,
to
,
to ![]() ,
zatem
,
zatem![]() .
Rozważając przykład dystrybucji określonej wzorem
.
Rozważając przykład dystrybucji określonej wzorem
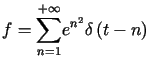 tzn
tzn 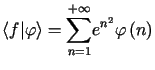 |
(9.8) |
widać, że jest ona poprawnie zdefiniowana dla ![]() (odpowiednia suma jest skończona, bowiem nośnik
(odpowiednia suma jest skończona, bowiem nośnik ![]() jest zwarty), natomiast nie jest określona np. dla
jest zwarty), natomiast nie jest określona np. dla ![]() (otrzymujemy nieskończony szereg rozbieżny
(otrzymujemy nieskończony szereg rozbieżny ![]() ).
W takim razie
).
W takim razie ![]() .
.
Przyjęcie powyższej definicji dystrybucji temperowanej jest uzasadnione tym, że w przypadku funkcji klasycznych (dystrybucji regularnych) dla uzyskania zbieżności całki postaci
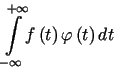 ,
,T w i e r d z e n i e (równość Parsevala)
Niech ![]() ,
, ![]() będą bezwzględnie całkowalne na
będą bezwzględnie całkowalne na ![]() .
Niech
.
Niech ![]() ,
, ![]() .
Wówczas zachodzi równość
.
Wówczas zachodzi równość
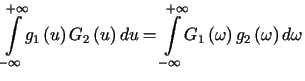 |
(9.9) |
Przekształcając lewą stronę wzoru (9.9) otrzymujemy
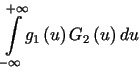 |
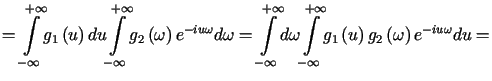 |
|
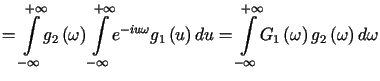 |
co kończy dowód.
Opierając się na powyższym twierdzeniu obowiązującym dla funkcji klasycznych
(dystrybucji regularnych) wprowadzamy definicję transformaty Fouriera dystrybucji
temperowanych.
D e f i n i c j a
Dla ![]() określamy
określamy
| (9.10) |
dla ![]() .
.
Następujące dwa twierdzenia uzasadniają poprawność przyjętej definicji.
T w i e r d z e n i e
Jeśli ![]() ,
to
,
to ![]() .
Ponadto
.
Ponadto ![]() jest ciągła.
jest ciągła.
Dla dowodu zauważmy, że jeśli ![]() ,
to
,
to ![]() jest całkowalna
na
jest całkowalna
na ![]() ,
zatem
,
zatem ![]() istnieje. Ze wzorów na transformatę Fouriera funkcji całkowalnych wynika,
że o ile
istnieje. Ze wzorów na transformatę Fouriera funkcji całkowalnych wynika,
że o ile![]() jest całkowalna (a tak jest dla funkcji
jest całkowalna (a tak jest dla funkcji![]() ),
to istnieje pochodna
),
to istnieje pochodna ![]() i zachodzi
i zachodzi
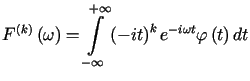
![$\displaystyle \left\vert \left( i\omega\right) ^{m}F^{\left( k\right) }\left(\...... \left( -it\right) ^{k}\varphi\left(t\right) \right] \right\vert dt\leq Const$](img1300.gif)
T w i e r d z e n i e
Jeśli ![]() ,
to jej transformata Fouriera
,
to jej transformata Fouriera ![]() .
.
Wystarczy wykazać, że ![]() jest liniowa i ciągła. Liniowość jest oczywista - wynika wprost z przyjętej
definicji. Ciągłość wynika z ciągłości transformaty Fouriera dla funkcji
szybkomalejących i ciągłości
jest liniowa i ciągła. Liniowość jest oczywista - wynika wprost z przyjętej
definicji. Ciągłość wynika z ciągłości transformaty Fouriera dla funkcji
szybkomalejących i ciągłości ![]() ,
ponieważ o ile
,
ponieważ o ile![]() w
w ![]() ,
to
,
to
=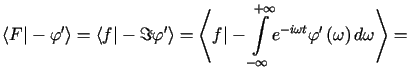 (całk. przez części)
(całk. przez części) |
||
![$\displaystyle =\left\langle f\vert-it{\displaystyle\int\limits_{-\infty}^{+\inf......e =\left\langle \Im\left[ -itf\left( t\right) \right] \vert\varphi\right\rangle$](img1311.gif) |
zatem ![]() .
.
![$\displaystyle =\left\langle D^{k}<tex2html_comment_mark>1455 f\vert\Im\varphi\r......t\Im\left[ \left( -it\right) ^{k}\varphi\left( t\right) \right] \right\rangle =$](img1315.gif) |
||
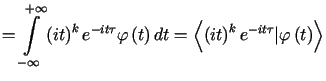 ,
zatem ,
zatem |
||
Wynika stąd, że w szczególności
![$\displaystyle \left\langle \Im\left[ 1\right] \vert\varphi\right\rangle =\left\......dt=2\pi\varphi\left( 0\right)=\left\langle 2\pi\delta\vert\varphi\right\rangle$](img1330.gif) .
.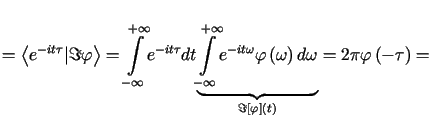 |
||
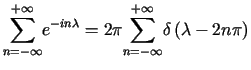 . . |
(9.11) |
Dowód
Niech ![]() .
Wówczas
.
Wówczas
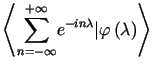 |
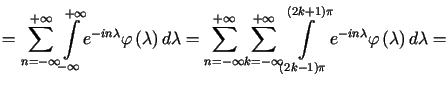 |
|
![$\displaystyle =\left\vert \begin{array}[c]{l}<tex2html_comment_mark>1513 \lambd......ts_{-\pi}^{+\pi}} e^{-in\left( r+2k\pi\right) }\varphi\left( r+2k\pi\right) dr=$](img1341.gif) |
||
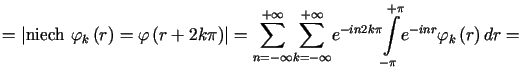 |
||
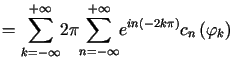 , , |
gdzie 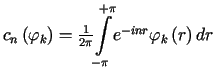 są współczynnikami Fouriera funkcji
są współczynnikami Fouriera funkcji ![]() .
Wyrażenie
.
Wyrażenie 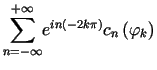 jest wartością sumy szeregu Fouriera tej funkcji w punkcie
jest wartością sumy szeregu Fouriera tej funkcji w punkcie ![]() ,
a zatem z okresowości tej sumy mamy
,
a zatem z okresowości tej sumy mamy
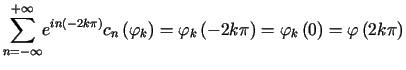 .
.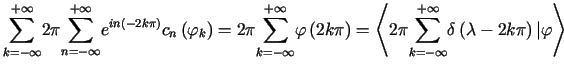
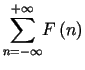 |
![$\displaystyle =\left\langle {\displaystyle\sum\limits_{n=-\infty}^{+\infty}} \d......y}^{+\infty}} \delta\left( \lambda-n\right) \right] \vert\varphi\right\rangle =$](img1350.gif) |
|
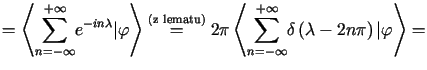 |
||
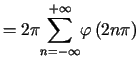 . . |
Udowodniony został zatem wzór
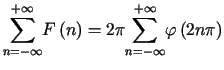 |
(9.12) |
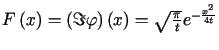 .
Stosując wzór sumacyjny Poissona otrzymujemy
.
Stosując wzór sumacyjny Poissona otrzymujemy
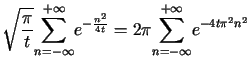 .
.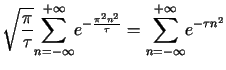 . . |
(9.13) |