



Next:Szeregi
Fouriera względem układówUp:Informacja
o przestrzeniach HilbertaPrevious:Ortogonalność,
twierdzenie o rzucieSpis
rzeczy
Subsections
Układy ortonormalne w przestrzeniach
Hilberta
W teorii przestrzeni Hilberta wielką rolę odgrywają tzw.
układy ortogonalne
i uklady ortonormalne. Pozwalają one znajdować rozwinięcia elementów
przestrzeni Hilberta na szeregi względem tych układów.
D e f i n i c j a
Układem ortogonalnym w przestrzeni Hilberta 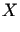 nazywamy zbiór
nazywamy zbiór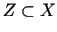 taki, że dla każdego
taki, że dla każdego 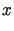 ,
, 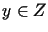 ,
, 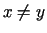 zachodzi
zachodzi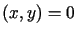 .
.
D e f i n i c j a
Układem ortonormalnym w przestrzeni Hilberta 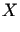 nazywamy układ ortogonalny
nazywamy układ ortogonalny 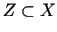 taki, że dla każdego
taki, że dla każdego 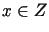 zachodzi
zachodzi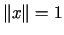 .
.
T w i e r d z e n i e
Niech 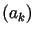 będzie dowolnym ciągiem liniowo niezależnych elementów przestrzeni Hilberta
będzie dowolnym ciągiem liniowo niezależnych elementów przestrzeni Hilberta 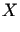 .
Istnieje wtedy w przestrzeni
.
Istnieje wtedy w przestrzeni 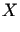 układ ortonormalny
układ ortonormalny 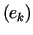 taki, że
taki, że
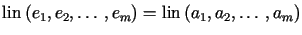 dla
dla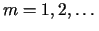 ,
gdzie
,
gdzie 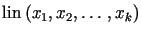 oznacza przestrzeń liniową wszystkich kombinacji liniowych elementów
oznacza przestrzeń liniową wszystkich kombinacji liniowych elementów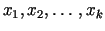 .
.
Dla dowodu wystarczy zastosować tzw. procedurę ortonormalizacji
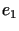 |
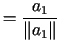 , , |
|
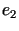 |
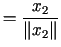 ,
gdzie ,
gdzie 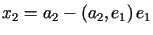 |
|
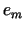 |
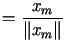 ,
gdzie ,
gdzie 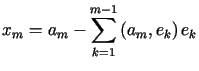 , , |
(10.15) |
z której bezpośrednio wynika, że 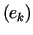 jest układem ortonormalnym spełniającym tezę twierdzenia.
jest układem ortonormalnym spełniającym tezę twierdzenia.
Przykłady układów ortonormalnych
-
Niech
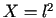 - zbiór ciągów nieskończonych
- zbiór ciągów nieskończonych 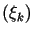 takich, że szereg
takich, że szereg 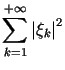 jest zbieżny, z iloczynem skalarnym
jest zbieżny, z iloczynem skalarnym 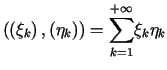 .
.
Wówczas elementy 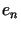 ,
gdzie
,
gdzie
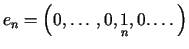 tworzą układ ortonormalny w
tworzą układ ortonormalny w 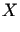 .
.
-
Niech
![$ X=L^{2}\left( \left[ 0;2\pi\right] \right) $](img1469.gif) (przestrzeń funkcji rzeczywistych całkowalnych z kwadratem).
(przestrzeń funkcji rzeczywistych całkowalnych z kwadratem).
Ciąg funkcji
tworzy układ ortonormalny w tej przestrzeni.
-
Niech
![$ X=L^{2}\left( \left[ 0;2\pi\right] \right) $](img1469.gif) (przestrzeń funkcji zespolonych całkowalnych z kwadratem).
(przestrzeń funkcji zespolonych całkowalnych z kwadratem).
Ciąg funkcji
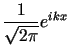 dla
dla 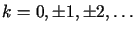 tworzy układ ortonormalny w tej przestrzeni (
tworzy układ ortonormalny w tej przestrzeni (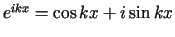 ).
).




Next:Szeregi
Fouriera względem układówUp:Informacja
o przestrzeniach HilbertaPrevious:Ortogonalność,
twierdzenie o rzucieSpis
rzeczy
Administrator 2003-03-01
![]() nazywamy zbiór
nazywamy zbiór![]() taki, że dla każdego
taki, że dla każdego ![]() ,
, ![]() ,
, ![]() zachodzi
zachodzi![]() .
.
![]() nazywamy układ ortogonalny
nazywamy układ ortogonalny ![]() taki, że dla każdego
taki, że dla każdego ![]() zachodzi
zachodzi![]() .
.
![]() będzie dowolnym ciągiem liniowo niezależnych elementów przestrzeni Hilberta
będzie dowolnym ciągiem liniowo niezależnych elementów przestrzeni Hilberta ![]() .
Istnieje wtedy w przestrzeni
.
Istnieje wtedy w przestrzeni ![]() układ ortonormalny
układ ortonormalny ![]() taki, że
taki, że
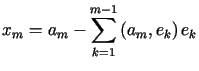 ,
,![]() jest układem ortonormalnym spełniającym tezę twierdzenia.
jest układem ortonormalnym spełniającym tezę twierdzenia.
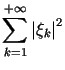 jest zbieżny, z iloczynem skalarnym
jest zbieżny, z iloczynem skalarnym 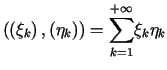 .
.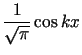 ,
, 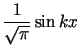 dla
dla 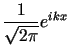 dla
dla