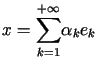 , , |
(10.17) |
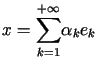 , , |
(10.17) |
gdzie ![]() jest układem ortonormalnym w
jest układem ortonormalnym w ![]() .
.
Mnożąc obie strony równości (10.17)
skalarnie przez ![]() i korzystając z ortonormalności układu
i korzystając z ortonormalności układu ![]() otrzymujemy, że
otrzymujemy, że
| (10.18) |
D e f i n i c j a
Liczby ![]() określone wzorem (10.18) nazywamy współczynnikami
Fouriera elementu
określone wzorem (10.18) nazywamy współczynnikami
Fouriera elementu ![]() względem układu ortonormalnego
względem układu ortonormalnego ![]() ,
a szereg
,
a szereg 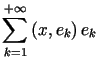 nazywamy szeregiem Fouriera elementu
nazywamy szeregiem Fouriera elementu![]() względem tego układu.
względem tego układu.
T w i e r d z e n i e
Jeśli ![]() jest układem ortonormalnym w przestrzeni Hilberta
jest układem ortonormalnym w przestrzeni Hilberta ![]() ,
to dla każdego
,
to dla każdego ![]() szereg
szereg 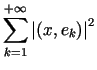 jest zbieżny i zachodzi nierówność
jest zbieżny i zachodzi nierówność
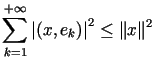 (tzw. nierówność Bessela),
(tzw. nierówność Bessela), |
(10.19) |
która staje się równością wtedy i tylko wtedy, gdy 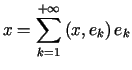 ,
tzn. gdy
,
tzn. gdy ![]() jest równy sumie swojego szeregu Fouriera.
jest równy sumie swojego szeregu Fouriera.
T w i e r d z e n i e
Jeśli ![]() jest układem ortonormalnym w przestrzeni Hilberta
jest układem ortonormalnym w przestrzeni Hilberta ![]() ,
to dla każdego
,
to dla każdego ![]() i dowolnych stałych
i dowolnych stałych ![]() zachodzi nierówność
zachodzi nierówność
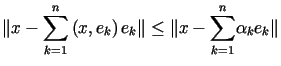 , , |
(10.20) |
która oznacza, że ![]() ta
suma częściowa szeregu Fouriera elementu
ta
suma częściowa szeregu Fouriera elementu ![]() jest najlepszym możliwym przybliżeniem tego elementu w podprzestrzeni
jest najlepszym możliwym przybliżeniem tego elementu w podprzestrzeni ![]() .
.
Dowód wynika z faktu, że 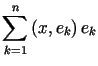 jest rzutem ortogonalnym elementu
jest rzutem ortogonalnym elementu ![]() na
na![]() .
.
Następne twierdzenie precyzuje warunki rozwijalności dowolnego elementu
przestrzeni Hilberta ![]() na szereg Fouriera względem układu ortonormalnego
na szereg Fouriera względem układu ortonormalnego ![]() .
.
T w i e r d z e n i e
Niech ![]() będzie układem ortonormalnym w przestrzeni Hilberta
będzie układem ortonormalnym w przestrzeni Hilberta ![]() .
Wówczas każdy element
.
Wówczas każdy element ![]() jest sumą swojego szeregu Fouriera (10.17)
wtedy i tylko wtedy, gdy układ
jest sumą swojego szeregu Fouriera (10.17)
wtedy i tylko wtedy, gdy układ![]() generuje całą przestrzeń
generuje całą przestrzeń ![]() .
.
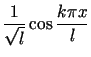 , , 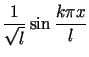 dla
dla |
(10.21) |
jest układem ortonormalnym w ![]() ,
generującym całą przestrzeń (por. przykład 2 i wzory (10.16)).
,
generującym całą przestrzeń (por. przykład 2 i wzory (10.16)).
Jeśli ![]() ,
to na mocy poprzedniego twierdzenia możemy napisać, że
,
to na mocy poprzedniego twierdzenia możemy napisać, że
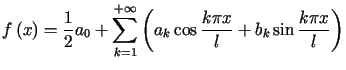 , , |
(10.22) |
gdzie
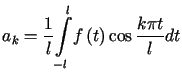 dla
dla |
(10.23) | |
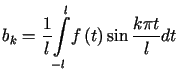 dla
dla |
(10.24) |
Zbieżność szeregu (10.22) w przestrzeni ![]() nie oznacza zbieżności w każdym punkcie
nie oznacza zbieżności w każdym punkcie ![]() .
Zgodnie z definicją normy, zbieżność w przestrzeni
.
Zgodnie z definicją normy, zbieżność w przestrzeni ![]() oznacza tylko, że
oznacza tylko, że
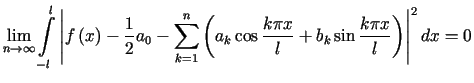 . . |
(10.25) |
W celu zagwarantowania zbieżności punktowej, należy założyć o funkcji danej pewne dodatkowe warunki.
D e f i n i c j a
Mówimy, że funkcja ![]() spełnia w przedziale
spełnia w przedziale ![]() warunki
Dirichleta wtedy i tylko wtedy, gdy:
warunki
Dirichleta wtedy i tylko wtedy, gdy:
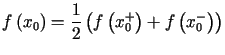 ,
,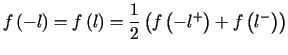 .
.Jeżeli funkcja ![]() spełnia w przedziale
spełnia w przedziale ![]() warunki Dirichleta, to w każdym punkcie tego przedziału jest ona sumą swojego
szeregu Fouriera (10.22).
warunki Dirichleta, to w każdym punkcie tego przedziału jest ona sumą swojego
szeregu Fouriera (10.22).