



Next:Ślady
funkcji z przestrzeniUp:Informacja
o przestrzeniach SobolewaPrevious:Informacja
o przestrzeniach SobolewaSpis
rzeczy
Definicja przestrzeni Sobolewa
Niech 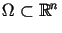 będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta
będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta 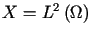 z iloczynem skalarnym zdefiniowanym równością (10.9)
i normą zdefiniowaną wzorem (10.10). W
tej przestrzeni rozważamy podzbiór składający się z funkcji f, których
pochodne cząstkowe w sensie dystrybucyjnym do rzędu m włącznie (patrz
również wzory (8.1)-(8.3))
należą do
z iloczynem skalarnym zdefiniowanym równością (10.9)
i normą zdefiniowaną wzorem (10.10). W
tej przestrzeni rozważamy podzbiór składający się z funkcji f, których
pochodne cząstkowe w sensie dystrybucyjnym do rzędu m włącznie (patrz
również wzory (8.1)-(8.3))
należą do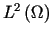 .
.
W podzbiorze takich funkcji wprowadzamy funkcjonał 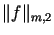 określony wzorem
określony wzorem
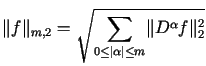 . . |
(11.1) |
Można pokazać, że 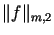 spełnia wszystkie aksjomaty normy.
spełnia wszystkie aksjomaty normy.
D e f i n i c j a
Przestrzenią Sobolewa 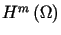 nazywamy zbiór
nazywamy zbiór
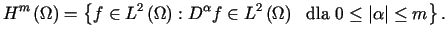 |
(11.2) |
T w i e r d z e n i e
Przestrzeń 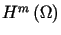 jest zupełna, jest zatem przestrzenią Hilberta. Funkcjonał
jest zupełna, jest zatem przestrzenią Hilberta. Funkcjonał 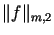 określa normę w
określa normę w 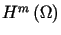 ,
zaś iloczyn skalarny zadany jest wzorem
,
zaś iloczyn skalarny zadany jest wzorem
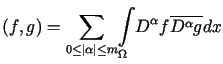 . . |
(11.3) |
U w a g a
Powyższą definicję przestrzeni Sobolewa można rozszerzyć na przypadek
przestrzeni 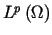 ,
w których norma zadana jest wzorem
,
w których norma zadana jest wzorem
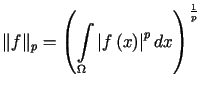 dla
dla 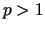 . . |
(11.4) |




Next:Ślady
funkcji z przestrzeniUp:Informacja
o przestrzeniach SobolewaPrevious:Informacja
o przestrzeniach SobolewaSpis
rzeczy
Administrator 2003-03-07
![]() określony wzorem
określony wzorem
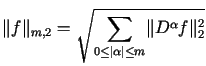 .
.![]() spełnia wszystkie aksjomaty normy.
spełnia wszystkie aksjomaty normy.
![]() nazywamy zbiór
nazywamy zbiór
![]() jest zupełna, jest zatem przestrzenią Hilberta. Funkcjonał
jest zupełna, jest zatem przestrzenią Hilberta. Funkcjonał ![]() określa normę w
określa normę w ![]() ,
zaś iloczyn skalarny zadany jest wzorem
,
zaś iloczyn skalarny zadany jest wzorem
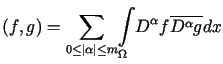 .
.![]() ,
w których norma zadana jest wzorem
,
w których norma zadana jest wzorem
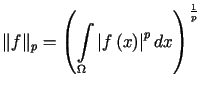 dla
dla