Spis rzeczy

Ślady funkcji z przestrzeni Sobolewa na powierzchniach

Niech $\Omega\subset\mathbb{R}^{n}$, $S\subset\Omega$ będzie powierzchnią $\left( n-1\right)$ wymiarową. Jeśli f jest funkcją, która w każdym punkcie$x\in\Omega$ ma jednoznacznie określoną wartość, to wyznacza ona w sposób naturalny funkcję $f_{\vert S}:=f\left( x\right)$ dla $x\in S$.

Jeśli natomiast funkcja f jest określona prawie wszędzie (tzn. z dokładnością do zbiorów miary zero), wtedy jej wartość na powierzchni S nie jest już wyznaczona w tak naturalny sposób, ponieważ $\left\vert S\right\vert =0$, gdzie $\left\vert S\right\vert$ oznacza $n-$wymiarową miarę Lebesgue'a powierzchni S. Oznacza to, że nie można prostym, naturalnym sposobem określić funkcji$f_{\vert S}$ za pomocą rozważenia wyłącznie wartości tej funkcji w pewnych punktach.

Dla prostoty załóżmy teraz, że $S=\overline{\Omega}\cap\left\{x_{n}=const\right\}$. Wówczas można udowodnić, że dla prawie wszystkich $x_{n}$ funkcja f (określona prawie wszędzie na $\Omega$) posiada wartość $f_{\vert S}$ zdefiniowaną prawie wszędzie jako funkcję $\left( n-1\right)$ zmiennych.

Wprowadzimy teraz bardziej sformalizowaną definicję śladu funkcji. Rozpoczniemy od przypadku funkcji f ciągłej na na$\overline{\Omega}$.
 

D e f i n i c j a

Śladem funkcji $f\in C\left( \overline{\Omega}\right)$ na $\left( n-1\right)$ wymiarowej powierzchni $S\subset\Omega$ nazywamy funkcję ciągłą na S, która prawie wszędzie pokrywa się z f. Ślad oznaczamy jako $f_{\vert S}$.

Rozważmy teraz funkcje f z przestrzeni Sobolewa $H^{1}\left(\Omega\right)$. Niech S będzie powierzchnią klasy$C^{1}$. Niech$S_{1}\subset S$ będzie częścią tej powierzchni reprezentowaną za pomocą przedstawienia

$$x_{n}=\varphi\left( x^{\prime}\right)$$, $$x^{\prime}=\left(x_{1},x_{2},\ldots,x_{n-1}\right)$$, $$\varphi^{\prime}\in C^{1}\left(\overline{D}\right)$$, $$D\subset\mathbb{R}^{n-1}$$. Załóżmy, że $\Omega$ zawarty jest w kostce $\left\{0<x_{i}<a\text{, \ dla }i=1,2,\ldots,n\right\}$. Załóżmy również chwilowo, że $f\in C_{0}^{1}\left( \overline{\Omega}\right)$ (zbiór funkcji klasy $C^{1}$ o nośniku zwartym). Wtedy $$f_{\vert S_{1}}\left( x\right) =f\left( x^{\prime},\varphi\left( ......tial f\left( x^{\prime},\xi_{n}\right) }{\partial\xi_{n}%%}d\xi_{n}\text{.}%%$$ Na mocy nierówności (10.11) możemy napisać, że $$\left\vert f_{\vert S_{1}}\left( x\right) \right\vert ^{2}\leq\va......\prime},\xi_{n}\right) }{\partial\xi_{n}%%}\right\vert ^{2}d\xi_{n}\text{.}%%$$ Mnożąc obustronnie powyższą nierówność przez$\sqrt{1+\varphi_{x_{1}}^{2}+\ldots+\varphi_{x_{n-1}}^{2}}$ i całkując po D dostajemy

$$\Vert f_{\vert S_{1}}\Vert_{L^{2}\left( S_{1}\right) } =<tex2html_comment_mark>1890 {\displaystyle\int\limits_{S_{1}}} \left\vert f_{\vert S_{1}}\left( x\right) \right\vert ^{2}dS_{1}=$$

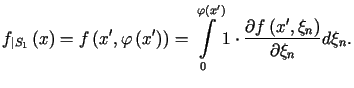
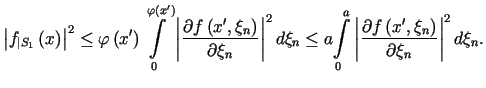
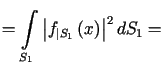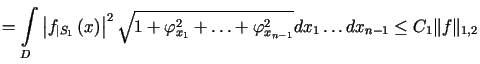$$=<tex2html_comment_mark>1894 {\displaystyle\int\limits_{D}} \left......dots+\varphi_{x_{n-1}}^{2}}dx_{1}\ldots dx_{n-1}\leq C_{1}\Vert f\Vert_{1,2}%%$$ (11.5)

gdzie $C_{1}$ jest stałą, która nie zależy od funkcji f tylko od obszaru $\Omega$ i powierzchni $S_{1}$ ($\Vert f\Vert_{1,2}$ oznacza normę w przestrzeni Sobolewa zdefiniowaną wzorem (11.1)).

Zakładając, że powierzchnia S składa się ze skończonej liczby powierzchni typu $S_{1}$ reprezentowanych przez różne przedstawienia, można wnioskować, że zachodzi nierówność postaci

$$\Vert f_{\vert S}\Vert_{L^{2}\left( S\right) }\leq C\Vert f\Vert_{1,2}<tex2html_comment_mark>1901%%$$ (11.6)

gdzie C zależy wyłącznie od obszaru $\Omega$ i powierzchni S. Przez aproksymację funkcji z przestrzeni $C^{1}\left( \Omega\right)$ funkcjami z $C_{0}^{1}\left( \Omega\right)$ łatwo pokazać, że powyższa nierówność zachodzi dla dowolnych funkcji $f\inC^{1}\left( \overline{\Omega}\right)$.

Przypuśćmy teraz, że $f\in H^{1}\left( \Omega\right)$. Wynika stąd, że istnieje ciąg $\left( f_{n}\right)$ funkcji klasy$C^{1}\left( \overline{\Omega}\right)$ taki, że $f_{n}\rightarrow f$ w normie $H^{1}\left(\Omega\right)$. Z nierówności (11.6) wynika, że

$$\Vert f_{n\vert S}-f_{m\vert S}\Vert_{L^{2}\left( S\right) }\leq C\Vert f_{n}%%-f_{m}\Vert_{1,2}$$, zatem ciąg śladów funkcji ciągłych $\left( f_{n\vert S}\right)$ jest ciągiem Cauchy'ego w $L^{2}\left( S\right)$. Z zupełności przestrzeni $L^{2}\left( S\right)$ wnioskujemy, ze istnieje funkcja$f_{\vert S}\in L^{2}\left( S\right)$ będąca granicą tego ciągu, tzn.

$$f_{\vert S}=\lim\limits_{n\rightarrow\infty}f_{n\vert S}$$ (11.7)

D e f i n i c j a

Funkcję $f_{\vert S}$ określoną równością (11.7) nazywamy śladem funkcji $f\in H^{1}\left( \Omega\right)$ na $\left( n-1\right)$ wymiarowej powierzchni S.

U w a g a

Można pokazać, że ślad funkcji z przestrzeni $H^{1}\left(\Omega\right)$ jest wyznaczony jednoznacznie. Za pomocą odpowiedniego przejścia granicznego możemy wywnioskować, że nierówność (11.6) zachodzi dla wszystkich funkcji $f\in H^{1}\left( \Omega\right)$, gdzie $f_{\vert S}$ oznacza ślad funkcji f na powierzchni S.
 

Poprzednie rozważania można sformułować w postaci następującego twierdzenia.
 

T w i e r d z e n i e

Niech $S\subset\Omega$ będzie $\left( n-1\right)$ wymiarową powierzchnią klasy $C^{1}$. Wówczas dowolna funkcja f z przestrzeni$H^{1}\left(\Omega\right)$ ma jednoznacznie określony ślad$f_{\vert S}$ na powierzchni S. Funkcja $f_{\vert S}$ należy do przestrzeni$L^{2}\left( S\right)$ i spełnia nierówność (11.6).

U w a g a   1

Analogicznie do poprzednich rozważań można pokazać, że jeśli $\alpha$ jest wielowskaźnikiem postaci $\alpha=\left(\alpha_{1},\alpha_{2},\ldots,\alpha_{n}\right)$ oraz $\left\vert \alpha\right\vert=a_{1}+\alpha_{2}+\ldots+\alpha_{n}$, to każda funkcja $f\in H^{\left\vert\alpha\right\vert +1}\left( \Omega\right)$ wyznacza jednoznacznie ślad pochodnej $D^{a}f_{\vert S}$ na powierzchni S, przy czym zachodzi nierówność

$$\Vert D^{\alpha}f_{\vert S}\Vert_{L^{2}\left( S\right) }\leq C\Vert f\Vert_{\left\vert \alpha\right\vert +1,2}$$ (11.8)

Oznacza to, że funkcje z przestrzeni $H^{k}\left( \Omega\right)$ wyznaczają na powierzchni S ślady pochodnych do rzędu $\left(k-1\right)$ włącznie.

U w a g a   2

Poprzednie twierdzenia mówią, że każda funkcja z przestrzeni$H^{1}\left(\Omega\right)$ wyznacza swój ślad na powierzchni S i ślad ten należy do przestrzeni $L^{2}\left( S\right)$. Powstaje pytanie, czy każda funkcja $v\in L^{2}\left( S\right)$ jest śladem pewnej funkcji z $H^{1}\left(\Omega\right)$. Odpowiedź na to pytanie jest negatywna. Już dla n=2 można podać przykład funkcji z przestrzeni $L^{2}\left( S\right)$, gdzie S jest okręgiem jednostkowym, która nie jest śladem żadnej funkcji z $H^{1}\left(\Omega\right)$, $\Omega$ - koło jednostkowe. Można natomiast pokazać, że zbiór śladów funkcji z $H^{1}\left(\Omega\right)$ jest gęsty w $L^{2}\left( S\right)$.

Dla badania rozwiązalności pewnych zagadnień brzegowych dla równań różniczkowych cząstkowych duże znaczenie mają następujące dwa twierdzenia dotyczące zachowania się funkcji z przestrzeni Sobolewa.

T w i e r d z e n i e

Dowolny zbiór ograniczony w przestrzeni $H^{1}\left(\Omega\right)$ jest prezwarty w przestrzeni $L^{2}\left(\Omega\right)$ (tzn. każdy ciąg funkcji $\left( f_{n}\right)$, których normy $\Vert f_{n}%%\Vert_{1,2}$ są wspólnie ograniczone przez pewną stałą zawiera podciąg zbieżny w przestrzeni $L^{2}\left(\Omega\right)$).

Dowód twierdzenia polega na wykorzystaniu charakteryzacji zbiorów prezwartych w$L^{2}\left(\Omega\right)$, której nie będziemy w tym miejscu omawiać.

T w i e r d z e n i e

Jeśli pewien zbiór funkcji jest ograniczony w przestrzeni$H^{1}\left(\Omega\right)$, wtedy zbiór ich śladów na $\left( n-1\right)$ wymiarowej powierzchni S klasy $C^{1}$ jest prezwarty w przestrzeni $L^{2}\left( S\right)$.

Dla dowodu twierdzenia wystarczy pokazać, że istnieją stałe$C_{1}$ i $C_{2}$ takie, że dla dowolnej liczby $\delta>0$ i dowolnej funkcji $f\in H^{1}\left( \Omega\right)$ zachodzi nierówność

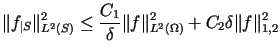$$\Vert f_{\vert S}\Vert_{L^{2}\left( S\right) }^{2}\leq\frac{C_{1}......a\right) }^{2}+C_{2}\delta\Vert f\Vert_{1,2}<tex2html_comment_mark>1931 ^{2}%%$$ (11.9)

i następnie skorzystać z poprzedniego twierdzenia.