| (14.1) |
| (14.1) |
w pewnej przestrzeni Hilberta ![]() .
Zakładamy, że operator
.
Zakładamy, że operator ![]() określony jest na pewnej podprzestrzeni liniowej
określony jest na pewnej podprzestrzeni liniowej ![]() i jego wartości leżą w
i jego wartości leżą w ![]() .
Na mocy twierdzenia o minimum funkcjonału kwadratowego (13.39)
wiemy, że jeśli równanie
.
Na mocy twierdzenia o minimum funkcjonału kwadratowego (13.39)
wiemy, że jeśli równanie ![]() jest spełnione dla
jest spełnione dla ![]() ,
tzn.
,
tzn. ![]() ,
to funkcjonał
,
to funkcjonał ![]() osiąga swoją najmniejszą wartość w
osiąga swoją najmniejszą wartość w ![]() w punkcie
w punkcie ![]() .
Nie wiadomo jednak, czy taki element
.
Nie wiadomo jednak, czy taki element ![]() istnieje.
istnieje.
Będziemy teraz usiłowali rozszerzyć ![]() do takiego zbioru, na którym funkcjonał
do takiego zbioru, na którym funkcjonał ![]() osiąga minimum.
osiąga minimum.
Załóżmy, że ![]() jest dodatnio określony, tzn. symetryczny oraz dla pewnej stałej
jest dodatnio określony, tzn. symetryczny oraz dla pewnej stałej ![]() zachodzi nierówność
zachodzi nierówność
| (14.2) |
W podprzestrzeni ![]() definiujemy nowy iloczyn skalarny określony wzorem
definiujemy nowy iloczyn skalarny określony wzorem
| (14.3) |
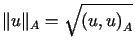 . . |
(14.4) |
Z założenia (14.2) wynika, że ![]() zatem ciągi zbieżne w normie
zatem ciągi zbieżne w normie ![]() są zbieżne także w normie standardowej
są zbieżne także w normie standardowej ![]() .
.
Niech teraz ![]() oznacza uzupełnienie
oznacza uzupełnienie ![]() w normie
w normie ![]() .
Przestrzeń liniową
.
Przestrzeń liniową ![]() nazywamy przestrzenią Friedrichsa generowaną przez operator
nazywamy przestrzenią Friedrichsa generowaną przez operator ![]() .
Można pokazać, że wzór (14.3) może być w
naturalny sposób rozszerzony dla wszystkich
.
Można pokazać, że wzór (14.3) może być w
naturalny sposób rozszerzony dla wszystkich![]() .
Podstawowe własności przestrzeni Friedrichsa opisuje następujące twierdzenie.
.
Podstawowe własności przestrzeni Friedrichsa opisuje następujące twierdzenie.
T w i e r d z e n i e
Przestrzeń ![]() jest przestrzenią Hilberta. Zbiór
jest przestrzenią Hilberta. Zbiór ![]() jest gęsty w
jest gęsty w ![]() ,
tzn. dowolny element z
,
tzn. dowolny element z![]() przestrzeni
przestrzeni ![]() może być przybliżony przez elementy z
może być przybliżony przez elementy z ![]() .
.
Rozważmy teraz funkcjonał ![]() .
Na mocy (14.3) może on być zapisany jako
.
Na mocy (14.3) może on być zapisany jako
| (14.5) |
Z poprzednich uwag wynika, że wzór (14.5)
jest w naturalny sposób określony na ![]() .
.
T w i e r d z e n i e
Niech operator ![]() będzie dodatnio określony na gęstej podprzestrzeni liniowej
będzie dodatnio określony na gęstej podprzestrzeni liniowej ![]() przestrzeni Hilberta
przestrzeni Hilberta ![]() .
Niech
.
Niech ![]() będzie przestrzenią Friedrichsa generowaną przez operator
będzie przestrzenią Friedrichsa generowaną przez operator ![]() .
Wówczas funkcjonał
.
Wówczas funkcjonał ![]() zdefiniowany na
zdefiniowany na ![]() za pomocą wzoru (14.5) przyjmuje na
za pomocą wzoru (14.5) przyjmuje na ![]() swoją najmniejszą wartość. Element
swoją najmniejszą wartość. Element ![]() ,
dla którego
,
dla którego ![]() osiąga swoją najmniejszą wartość jest wyznaczony jednoznacznie.
osiąga swoją najmniejszą wartość jest wyznaczony jednoznacznie.
Dla dowodu twierdzenia wystarczy zauważyć, że dla ustalonego ![]() wyrażenie
wyrażenie ![]() jest ciągłym funkcjonałem liniowym na
jest ciągłym funkcjonałem liniowym na ![]() ,
ponieważ na mocy (14.2) zachodzi nierówność
,
ponieważ na mocy (14.2) zachodzi nierówność
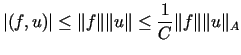 .
.| (14.6) |
D e f i n i c j a
Element ![]() minimalizujący funkcjonał (14.5) nazywamy
rozwiązaniem uogólnionym równania
minimalizujący funkcjonał (14.5) nazywamy
rozwiązaniem uogólnionym równania ![]() .
.
U w a g a 1
Równość ![]() nie prowadzi do efektywnego algorytmu skonstruowania rozwiązania
nie prowadzi do efektywnego algorytmu skonstruowania rozwiązania ![]() .
W celu znalezienia przybliżeń rozwiązania należy rozpatrzyć zagadnienie
minimalizacji funkcjonału
.
W celu znalezienia przybliżeń rozwiązania należy rozpatrzyć zagadnienie
minimalizacji funkcjonału ![]() .
.
U w a g a 2
Łatwo zauważyć, że jeśli
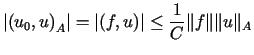 ,
,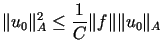 ,
a zatem ,
a zatem 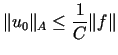 . . |
(14.7) |
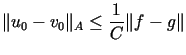 |
(14.8) |
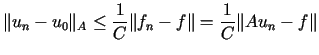 , , |
(14.9) |
U w a g a 3
Jeśli ![]() minimalizuje
minimalizuje ![]() na
na ![]() ,
to
,
to![]() jest rozwiązaniem zagadnienia
jest rozwiązaniem zagadnienia ![]() .
Jeśli jednak
.
Jeśli jednak![]() ,
to równanie
,
to równanie ![]() nie posiada rozwiązań w
nie posiada rozwiązań w![]() .
.
Istotnie, gdyby ![]() było rozwiązaniem równania
było rozwiązaniem równania ![]() w
w![]() ,
to
,
to ![]() byłoby najmniejszą wartością funkcjonału
byłoby najmniejszą wartością funkcjonału ![]() w
w ![]() .
Ponieważ jednak
.
Ponieważ jednak