



Next:Metoda
RitzaUp:Wstęp
do metod przybliżonychPrevious:Wariacyjna
definicja rozwiązań uogólnionychSpis
rzeczy
Metoda szeregów ortonormalnych
Rozważamy równanie (14.1) w pewnej przestrzeni
Hilberta  .
Zakładamy, że operator
.
Zakładamy, że operator 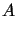 jest dodatnio określony na pewnej gęstej podprzestrzeni liniowej
jest dodatnio określony na pewnej gęstej podprzestrzeni liniowej 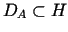 i jego wartości leżą w
i jego wartości leżą w  .
Na mocy twierdzenia o minimum funkcjonału kwadratowego (13.39)
wiemy, że jeśli równanie
.
Na mocy twierdzenia o minimum funkcjonału kwadratowego (13.39)
wiemy, że jeśli równanie 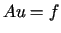 jest spełnione dla
jest spełnione dla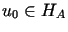 ,
tzn.
,
tzn. 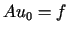 ,
to funkcjonał
,
to funkcjonał 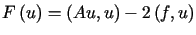 osiąga swoją najmniejszą wartość w
osiąga swoją najmniejszą wartość w 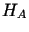 w punkcie
w punkcie 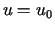 .
.
Zakładamy również, że przestrzeń 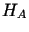 jest ośrodkowa (wystarczy żądać by
jest ośrodkowa (wystarczy żądać by  była ośrodkowa, np.
była ośrodkowa, np. 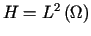 ).
).
Niech 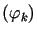 będzie układem ortonormalnym zupełnym w
będzie układem ortonormalnym zupełnym w 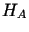 .
Wówczas zgodnie z teorią szeregów Fouriera w przestrzeniach Hilberta i
równością (10.17),
.
Wówczas zgodnie z teorią szeregów Fouriera w przestrzeniach Hilberta i
równością (10.17), 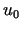 można przedstawić jako
można przedstawić jako
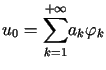 ,
gdzie ,
gdzie 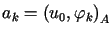 . . |
(14.10) |
Z definicji iloczynu skalarnego 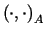 wynika, że
wynika, że
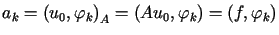 dla
dla 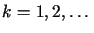 |
(14.11) |
Ze zbieżności szeregu (14.10) w 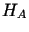 wynika jego zbieżność w
wynika jego zbieżność w  ,
ponieważ
,
ponieważ
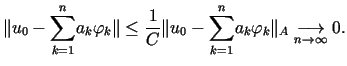 Powyższe rozważania można sformułować w postaci następującego twierdzenia.
Powyższe rozważania można sformułować w postaci następującego twierdzenia.
T w i e r d z e n i e
Niech 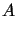 będzie operatorem dodatnio określonym na podprzestrzeni liniowej, gęstej
będzie operatorem dodatnio określonym na podprzestrzeni liniowej, gęstej 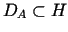 ,
, 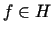 .
Niech
.
Niech 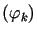 będzie układem ortonormalnym zupełnym w
będzie układem ortonormalnym zupełnym w 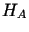 .
Wówczas rozwiązanie uogólnione
.
Wówczas rozwiązanie uogólnione 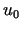 równania
równania 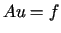 jest dane jako szereg (14.10) ze współczynnikami
określonymi wzorami (14.11).
jest dane jako szereg (14.10) ze współczynnikami
określonymi wzorami (14.11).
Niedogodnością metody szeregów ortonormalnych jest jest trudność efektywnego
uzyskania układów ortonormalnych zupełnych (tzw. baz ortonormalnych) w 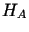 .
.




Next:Metoda
RitzaUp:Wstęp
do metod przybliżonychPrevious:Wariacyjna
definicja rozwiązań uogólnionychSpis
rzeczy
Administrator 2003-04-24
![]() będzie układem ortonormalnym zupełnym w
będzie układem ortonormalnym zupełnym w ![]() .
Wówczas zgodnie z teorią szeregów Fouriera w przestrzeniach Hilberta i
równością (10.17),
.
Wówczas zgodnie z teorią szeregów Fouriera w przestrzeniach Hilberta i
równością (10.17), ![]() można przedstawić jako
można przedstawić jako
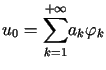 ,
gdzie
,
gdzie ![]() wynika jego zbieżność w
wynika jego zbieżność w ![]() ,
ponieważ
,
ponieważ
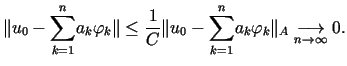
![]() będzie operatorem dodatnio określonym na podprzestrzeni liniowej, gęstej
będzie operatorem dodatnio określonym na podprzestrzeni liniowej, gęstej ![]() ,
, ![]() .
Niech
.
Niech ![]() będzie układem ortonormalnym zupełnym w
będzie układem ortonormalnym zupełnym w ![]() .
Wówczas rozwiązanie uogólnione
.
Wówczas rozwiązanie uogólnione ![]() równania
równania ![]() jest dane jako szereg (14.10) ze współczynnikami
określonymi wzorami (14.11).
jest dane jako szereg (14.10) ze współczynnikami
określonymi wzorami (14.11).
![]() .
.