



Next:Metoda
najmniejszych kwadratówUp:Wstęp
do metod przybliżonychPrevious:Metoda
RitzaSpis
rzeczy
Metoda Galerkina
Niech 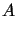 będzie operatorem określonym na
będzie operatorem określonym na 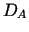 ,
, 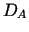 gęsty w
gęsty w ,
,  - ośrodkowa przestrzeń Hilberta. Rozważmy bazę
- ośrodkowa przestrzeń Hilberta. Rozważmy bazę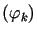 w
w 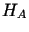 taką, że
taką, że 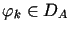 dla
dla 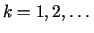 .
Nie zakładamy ortogonalności tego układu.
.
Nie zakładamy ortogonalności tego układu.
Poszukujemy przybliżenia rozwiązania uogólnionego równania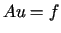 w postaci
w postaci
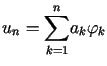 ,
gdzie stałe
,
gdzie stałe 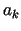 wyznaczamy z układu równań
wyznaczamy z układu równań
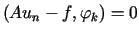 dla
dla 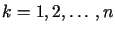 . . |
(14.16) |
Z gęstości 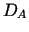 w
w  wynika, że gdyby warunek (14.16) spełniony
był dla wszystkich
wynika, że gdyby warunek (14.16) spełniony
był dla wszystkich 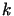 ,
to
,
to 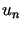 byłoby rozwiązaniem równania
byłoby rozwiązaniem równania 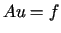 .
Ciąg
.
Ciąg 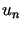 nazywamy ciągiem przybliżeń Galerkina.
nazywamy ciągiem przybliżeń Galerkina.
W przypadku, gdy operator 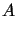 jest liniowy warunek (14.16) prowadzi do
układu równań
jest liniowy warunek (14.16) prowadzi do
układu równań
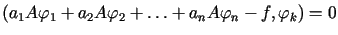 dla
dla 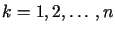 . . |
(14.17) |
tzn. w postaci rozwiniętej
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2893 \left(......\varphi _{n}\right) a_{n} & =\left( f,\varphi_{n}\right) \end{array} \right.%%$](img2087.gif) |
(14.18) |
Jeśli dodatkowo założymy, że 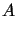 jest operatorem dodatnio określonym (a więc symetrycznym), to łatwo zauważyć,
że układ (14.18) jest identyczny z układem
równań (14.15) otrzymanym w wyniku stosowania
metody Ritza. W tym przypadku otrzymane ciągi przybliżeń są identyczne.
jest operatorem dodatnio określonym (a więc symetrycznym), to łatwo zauważyć,
że układ (14.18) jest identyczny z układem
równań (14.15) otrzymanym w wyniku stosowania
metody Ritza. W tym przypadku otrzymane ciągi przybliżeń są identyczne.
T w i e r d z e n i e
Niech 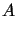 będzie operatorem dodatnio określonym na
będzie operatorem dodatnio określonym na 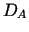 ,
, 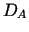 gęsty w
gęsty w  ,
, 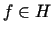 ,
,  - ośrodkowa przestrzeń Hilberta. Niech
- ośrodkowa przestrzeń Hilberta. Niech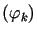 będzie bazą w
będzie bazą w 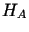 (niekoniecznie ortogonalną) oraz
(niekoniecznie ortogonalną) oraz 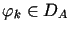 dla
dla 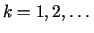 .
Wówczas ciąg przybliżeń Galerkina, gdzie stałe
.
Wówczas ciąg przybliżeń Galerkina, gdzie stałe 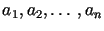 są wyznaczone z układu równań (14.18) jest
zbieżny w
są wyznaczone z układu równań (14.18) jest
zbieżny w 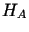 do rozwiązania uogólnionego równania
do rozwiązania uogólnionego równania 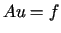 .
.
U w a g a 1 (porównanie z metodą Ritza)
Zakres stosowania metody Galerkina jest o wiele szerszy niż metody Ritza.
Dla zastosowania warunku (14.16) nie jest
konieczne, aby operator 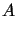 był dodatnio określony, symetryczny ani nawet liniowy. W metodzie Galerkina
punktem wyjścia jest równanie
był dodatnio określony, symetryczny ani nawet liniowy. W metodzie Galerkina
punktem wyjścia jest równanie 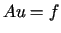 ,
zaś w metodzie Ritza - minimalizacja funkcjonału
,
zaś w metodzie Ritza - minimalizacja funkcjonału 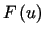 .
.
U w a g a 2
Można rozważać dwie różne bazy w przestrzeni 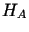 ,
tzn.
,
tzn.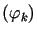 i
i 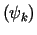 .
Poszukujemy przybliżenia rozwiązania uogólnionego równania
.
Poszukujemy przybliżenia rozwiązania uogólnionego równania 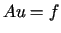 ,
podobnie jak poprzednio, w postaci
,
podobnie jak poprzednio, w postaci
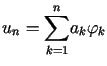 ,
gdzie stałe
,
gdzie stałe 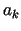 wyznaczamy z warunku
wyznaczamy z warunku
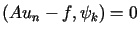 dla
dla 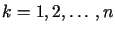 . . |
(14.19) |
Metoda ta nosi nazwę metody Galerkina-Pietrowa.




Next:Metoda
najmniejszych kwadratówUp:Wstęp
do metod przybliżonychPrevious:Metoda
RitzaSpis
rzeczy
Administrator 2003-04-24
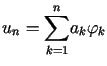 ,
,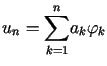 ,
,![]() jest liniowy warunek (14.16) prowadzi do
układu równań
jest liniowy warunek (14.16) prowadzi do
układu równań
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2893 \left(......\varphi _{n}\right) a_{n} & =\left( f,\varphi_{n}\right) \end{array} \right.%%$](img2087.gif)
![]() będzie operatorem dodatnio określonym na
będzie operatorem dodatnio określonym na ![]() ,
, ![]() gęsty w
gęsty w ![]() ,
, ![]() ,
, ![]() - ośrodkowa przestrzeń Hilberta. Niech
- ośrodkowa przestrzeń Hilberta. Niech![]() będzie bazą w
będzie bazą w ![]() (niekoniecznie ortogonalną) oraz
(niekoniecznie ortogonalną) oraz ![]() dla
dla ![]() .
Wówczas ciąg przybliżeń Galerkina, gdzie stałe
.
Wówczas ciąg przybliżeń Galerkina, gdzie stałe ![]() są wyznaczone z układu równań (14.18) jest
zbieżny w
są wyznaczone z układu równań (14.18) jest
zbieżny w ![]() do rozwiązania uogólnionego równania
do rozwiązania uogólnionego równania ![]() .
.
![]() był dodatnio określony, symetryczny ani nawet liniowy. W metodzie Galerkina
punktem wyjścia jest równanie
był dodatnio określony, symetryczny ani nawet liniowy. W metodzie Galerkina
punktem wyjścia jest równanie ![]() ,
zaś w metodzie Ritza - minimalizacja funkcjonału
,
zaś w metodzie Ritza - minimalizacja funkcjonału ![]() .
.
![]() ,
tzn.
,
tzn.![]() i
i ![]() .
Poszukujemy przybliżenia rozwiązania uogólnionego równania
.
Poszukujemy przybliżenia rozwiązania uogólnionego równania ![]() ,
podobnie jak poprzednio, w postaci
,
podobnie jak poprzednio, w postaci
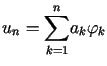 ,
,