Niech ![]() .
Rozwiązaniem uogólnionym zagadnienia
.
Rozwiązaniem uogólnionym zagadnienia ![]() jest taki punkt
jest taki punkt ![]() ,
że
,
że
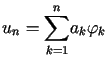 .
.
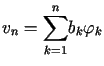 .
.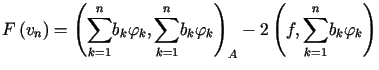 . . |
(14.12) |
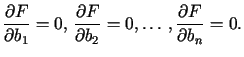
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2868 \left(......rphi_{n}\right) _{A}b_{n} & =\left( f,\varphi_{n}\right) \end{array} \right.%%$](img2071.gif) |
(14.13) |
Wyznacznik układu (14.13) jest różny
od zera, ponieważ elementy ![]() są liniowo niezależne (jest to tzw. wyznacznik Grama układu
są liniowo niezależne (jest to tzw. wyznacznik Grama układu ![]() ),
a więc wartości
),
a więc wartości![]() są jednoznacznie określone. W przypadku, gdy
są jednoznacznie określone. W przypadku, gdy ![]() jest układem ortonormalnym otrzymujemy natychmiast, że
jest układem ortonormalnym otrzymujemy natychmiast, że
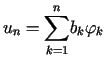 nazywamy ciągiem Ritza.
nazywamy ciągiem Ritza.
T w i e r d z e n i e
Niech ![]() będzie operatorem dodatnio określonym na
będzie operatorem dodatnio określonym na ![]() ,
,![]() gęste w
gęste w ![]() ,
, ![]() ,
, ![]() - ośrodkowa przestrzeń Hilberta. Niech
- ośrodkowa przestrzeń Hilberta. Niech ![]() będzie bazą w
będzie bazą w ![]() (niekoniecznie ortogonalną). Wówczas ciąg Ritza
(niekoniecznie ortogonalną). Wówczas ciąg Ritza ![]() ze współczynnikami
ze współczynnikami ![]() określonymi jednoznacznie przez układ równań (14.13)
zbiega w
określonymi jednoznacznie przez układ równań (14.13)
zbiega w ![]() (a więc i w
(a więc i w ![]() )
do uogólnionego rozwiązania
)
do uogólnionego rozwiązania![]() równania
równania ![]() .
.
U w a g a 1
Chociaż dla ciągu Ritza ![]() ,
to nie musi zachodzić
,
to nie musi zachodzić ![]() .
.
U w a g a 2
Korzystając z nierówności (10.20) i
własności przestrzeni Hilberta, można pokazać, że dla ![]() zachodzi zawsze nierówność
zachodzi zawsze nierówność
| (14.14) |
U w a g a 3
Jeśli elementy bazy ![]() należą do
należą do![]() ,
to układ równań (14.13) można zapisać w
postaci
,
to układ równań (14.13) można zapisać w
postaci
![$\displaystyle \left\{ \begin{array}[c]{ccccc}<tex2html_comment_mark>2883 \left(......\varphi _{n}\right) b_{n} & =\left( f,\varphi_{n}\right) \end{array} \right.%%$](img2080.gif) |
(14.15) |