What is GGP?

General Game Playing (GGP) is a research area concerned with a design of autonomous programs capable of playing a variety of games, including the ones they have never encountered before. This project refers to the particular embodiment of the GGP idea proposed by Stanford University in 2005. Since then, an annual GGP competition has been organized, that brings an additional challenge, excitement and the way to define the current trends in the field. The competitors, i.e. computer programs, are given the rules of games at run-time and have to figure out how to play without any human intervention. Therefore, they need to combine various interesting aspect such as knowledge extraction and representation, efficient state-search, abstract reasoning and decision making.

Here are some good introductions to the problem:

• http://logic.stanford.edu/ggp/chapters/chapter_01.html
• http://games.stanford.edu/index.php/what-is-ggp
• http://www.general-game-playing.de/
• http://www.ggp.org/docs/BeginnersGuide.html

The rules are written in the so-called Game Description Language (GDL). Any finite, deterministic, perfect-information synchronous game can be encoded in GDL. The official language specification can be found here.

What is MINI-Player

MINI-Player is our GGP agent. It was the first player from Poland (ax-aequo with Magician) to participate in the GGP Competition and the first one to reach the final day of this tournament (in 2012). 

In 2012, MINI-Player has advanced to the final day of the completion with the 5^th best score. The final place was 7^th. In 2013, it encountered some issues with single-player games and ended the tournament as 11-th not qualifying to the final day. In 2014, there were a record number of 49 players submitted to the qualifying round of the competition thanks to a massive online open course about GGP. Our player, together with 16 other ones, successfully went through the qualification round. Then it reach the final day with 11 other players. It managed to eliminate one opponent (2-0) but lost against two (1-2, 1-2) in a double-elimination format and finished the competition on the 7-8^th place.

The major parts and contributions of MINI-Player:

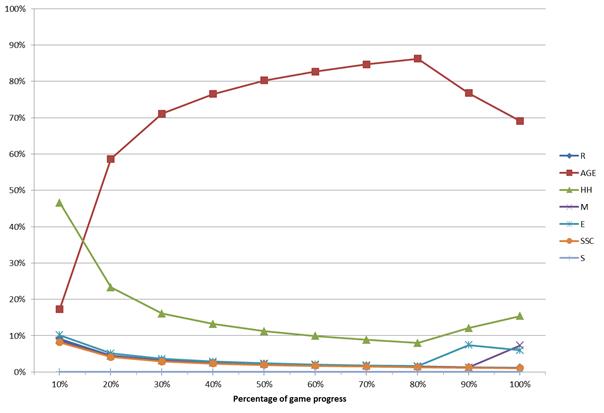
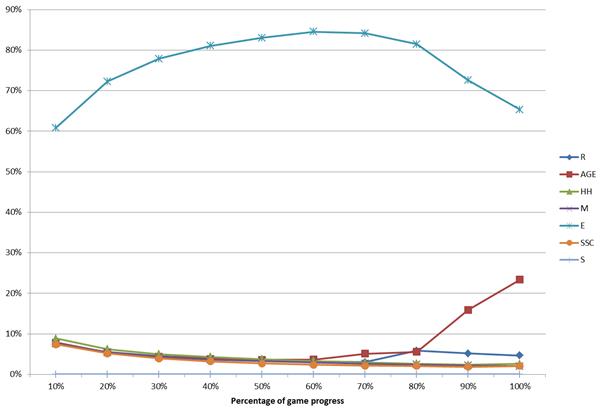
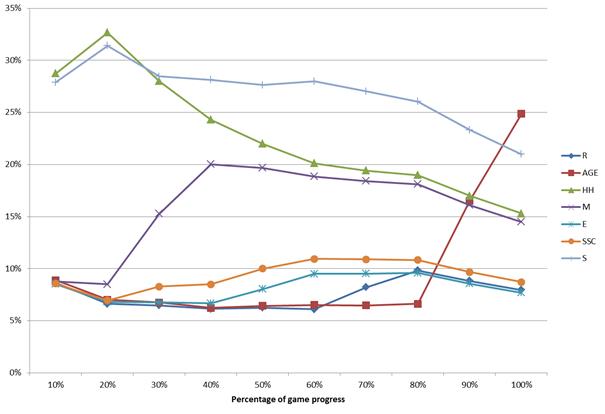
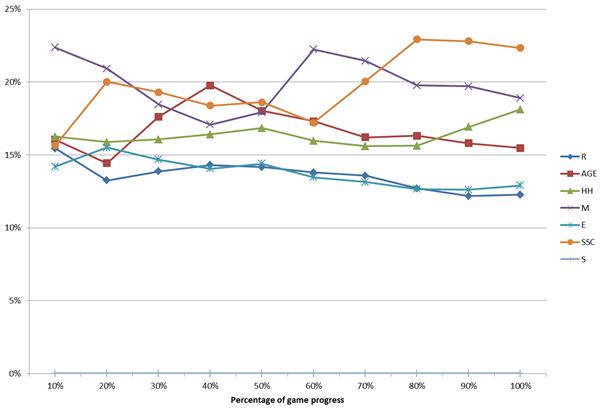
• A portfolio of the so-called strategies, which guide the Monte Carlo phase in the MCTS algorithm. In MINI-Player, seven strategies called: were implemented.
• Dynamic self-adaptation of the strategies based on their performance in a currently played game
• New method of parallelization of the MCTS/UCT algorithm in GGP
• A dedicated approach for single-player games
• A high-performance interpreter for the Game Description Language
• Communication module to take part in the GGP competition

In order to illustrate the way the MCTS algorithm works, let us consider a game between two MCTS-based machine players in a well-known game of Connect-4. In each step, each of the players was allotted 7 second for a move. Four interesting steps were selected from the played game. The following figure shows snapshots of the game board taken in these four steps (after the move was performed). The statistics computed for each available action (move) just prior to the presented game positions are provided below in the text. Please note that Q and N denote the parameters from the UCT formula. The boundary values of Q are equal to 0 (expected loss for red) and 100 (expected victory for red), respectively.

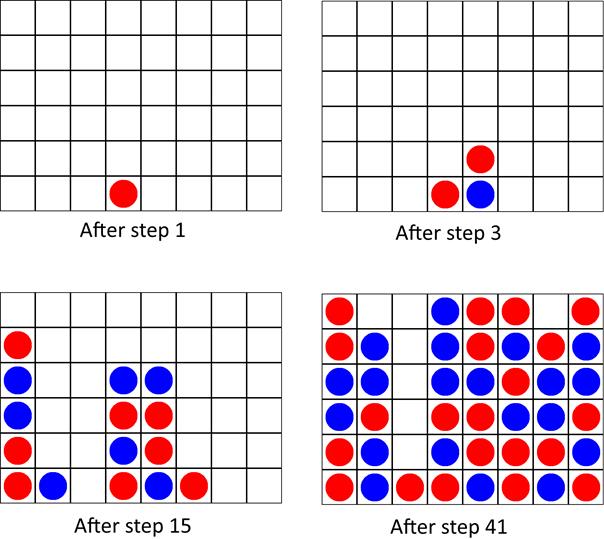
In step 1, two moves putting stones in the middlemost columns, i.e., 4 and 5, were clearly the best for the red player.

In step 3, the best strategy for red was to continue putting stones in the middle and block the blue player:

In step 15, the highest Q value was equal to 55.6, which means that the red player was slightly more likely to win, but the MCTS/UCT algorithm does not see any path leading to a very strong position (very likely victory) of this player (and of the other, as well):

Finally, in step 41, three out of four actions were assigned Q = 100 meaning that they lead to a victory for red. Only the last action resulted in an immediate win, but the length of a winning path makes no difference to the MCTS/UCT assessment.

Example games and selected results

As stated before, games in GGP are written in a GDL language. The language is based on Datalog and Prolog. Here, you can download [82KB] a compressed file with games used by us for the testing purposes.

The most famous public repositories can be found here:

http://www.ggp.org/view/tiltyard/games/

http://ggpserver.general-game-playing.de/ggpserver/public/show_games.jsp

http://arrogant.stanford.edu/ggp/php/showgames

The GGP competition is a specific testing environment as it is organized only once a year and very few matches between the players of a given match are carried out. Typically, a pair of GGP agents face each other from 2-4 times during a single day of the competition. Moreover, the choice of games is arbitrary and quite limited, so the luck/random factor plays a larger role than in a typical offline experiment with many repetitions. We have performed various experiments including MINI-Player that were carried out using 250 repetitions. We report the average scores obtained by MINI-Player, which is normalized into the [0,100] interval, where 0 is interpreted as a loss, 50 as a draw and 100 as a win of MINI-Player. Therefore, the higher the score, the better. For statistical significance we used the 95% confidence intervals computed from t-student distribution. They are presented as one number V, which should be interpreted that the score is burdened with the error of [–V, +V] with 95% statistical confidence.

TABLE 1

In the following table, the results achieved by MINI-Player against the basic implementation of the MCTS/UCT player are presented. Since the same basis is used in MINI-Player, the experiment reveals insights about the novel contributions, which are: portfolio of strategies and the mechanism of choosing a strategy for a simulation. Depending on the game, both players were given from 45 to 90 seconds for the initial analysis of the rules and from 10 to 30 seconds for making a move.