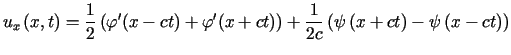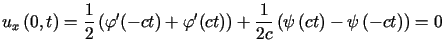Next:Wzór
KirchhoffaUp:Struna
nieograniczonaPrevious:Stabilność
rozwiązaniaSpis
rzeczy
Subsections
Struna jednostronnie ograniczona
Rozważmy zagadnienie polegające na znalezieniu rozwiązania równania drgań
półograniczonej struny swobodnej
z warunkami początkowymi
Struna z zamocowanym końcem
W tym przypadku poszukujemy funkcji 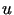 spełniającej dodatkowy warunek
spełniającej dodatkowy warunek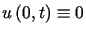 .
O funkcjach danych
.
O funkcjach danych 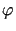 i
i 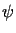 założymy, że spełniają one tzw. warunki zgodności
założymy, że spełniają one tzw. warunki zgodności
Dodatkowo zakładamy, że 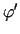 ,
, 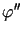 ,
,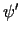 są ciągłe na półprostej
są ciągłe na półprostej 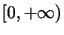 .
.
W celu rozwiązania powyższego zagadnienia, funkcje 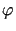 i
i 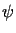 przedłużamy do funkcji nieparzystych określonych na całej osi rzeczywistej.
Warunki (2.12) gwarantują ciągłość otrzymanych
przedłużeń. Następnie, dla tak określonych przedłużeń, stosujemy wzór d'Alemberta
dla struny swobodnej (2.5)
przedłużamy do funkcji nieparzystych określonych na całej osi rzeczywistej.
Warunki (2.12) gwarantują ciągłość otrzymanych
przedłużeń. Następnie, dla tak określonych przedłużeń, stosujemy wzór d'Alemberta
dla struny swobodnej (2.5)
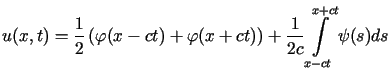 . . |
(2.13) |
Podstawiając 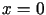 otrzymujemy
otrzymujemy
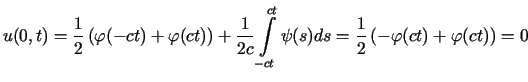 na mocy nieparzystości funkcji danych
na mocy nieparzystości funkcji danych 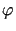 i
i 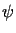 .
Oznacza to, że
.
Oznacza to, że 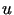 jest rozwiązaniem zagadnienia drgań struny z zamocowanym końcem.
jest rozwiązaniem zagadnienia drgań struny z zamocowanym końcem.
Struna ze swobodnym poziomym
końcem
Rozważamy zagadnienie polegające na wyznaczeniu rozwiązania 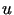 ,
spełniającego dodatkowo warunek
,
spełniającego dodatkowo warunek 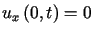 (koniec struny może poruszać się swobodnie w pionie, np. w prowadnicy dla
(koniec struny może poruszać się swobodnie w pionie, np. w prowadnicy dla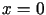 ).
O funkcjach danych
).
O funkcjach danych 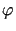 i
i 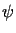 założymy, że spełniają one tzw. warunki zgodności
założymy, że spełniają one tzw. warunki zgodności
Zakładamy również, że 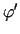 ,
, 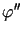 ,
, 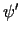 są ciągłe na półprostej
są ciągłe na półprostej 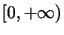 .
.
W celu rozwiązania powyższego zagadnienia, funkcje 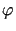 i
i 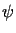 przedłużamy do funkcji parzystych określonych na całej osi rzeczywistej
(wówczas pochodna
przedłużamy do funkcji parzystych określonych na całej osi rzeczywistej
(wówczas pochodna 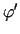 jest nieparzysta). Stosując podobnie jak poprzednio, wzór d'Alemberta (2.5)
przedstawiamy rozwiązanie
jest nieparzysta). Stosując podobnie jak poprzednio, wzór d'Alemberta (2.5)
przedstawiamy rozwiązanie 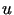 w postaci (2.13).
w postaci (2.13).
Wynika stąd, że
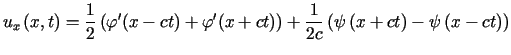 oraz
oraz
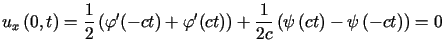 na mocy nieparzystości funkcji
na mocy nieparzystości funkcji 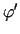 i parzystości funkcji
i parzystości funkcji 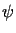 .
Oznacza to, że
.
Oznacza to, że 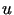 jest rozwiązaniem rozważanego zagadnienia.
jest rozwiązaniem rozważanego zagadnienia.




Next:Wzór
KirchhoffaUp:Struna
nieograniczonaPrevious:Stabilność
rozwiązaniaSpis
rzeczy
Administrator 2003-01-24
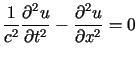 dla
dla 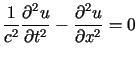 dla
dla ![]() ,
, ![]() ,
,![]() są ciągłe na półprostej
są ciągłe na półprostej ![]() .
.
![]() i
i ![]() przedłużamy do funkcji nieparzystych określonych na całej osi rzeczywistej.
Warunki (2.12) gwarantują ciągłość otrzymanych
przedłużeń. Następnie, dla tak określonych przedłużeń, stosujemy wzór d'Alemberta
dla struny swobodnej (2.5)
przedłużamy do funkcji nieparzystych określonych na całej osi rzeczywistej.
Warunki (2.12) gwarantują ciągłość otrzymanych
przedłużeń. Następnie, dla tak określonych przedłużeń, stosujemy wzór d'Alemberta
dla struny swobodnej (2.5)
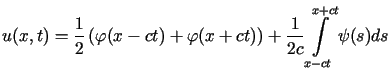 .
.![]() otrzymujemy
otrzymujemy
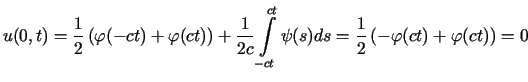
![]() ,
, ![]() ,
, ![]() są ciągłe na półprostej
są ciągłe na półprostej ![]() .
.
![]() i
i ![]() przedłużamy do funkcji parzystych określonych na całej osi rzeczywistej
(wówczas pochodna
przedłużamy do funkcji parzystych określonych na całej osi rzeczywistej
(wówczas pochodna ![]() jest nieparzysta). Stosując podobnie jak poprzednio, wzór d'Alemberta (2.5)
przedstawiamy rozwiązanie
jest nieparzysta). Stosując podobnie jak poprzednio, wzór d'Alemberta (2.5)
przedstawiamy rozwiązanie ![]() w postaci (2.13).
w postaci (2.13).