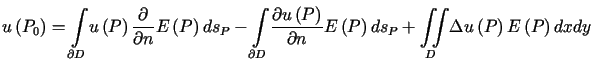 , , |
(7.7) |
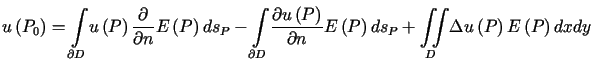 , , |
(7.7) |
gdzie, zgodnie z (6.7)
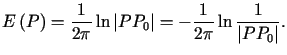
![$\displaystyle u\left( P_{0}\right) =-\frac{1}{2\pi}<tex2html_comment_mark>966 {...... PP_{0}\right\vert }\frac{\partial u\left( P\right) }{\partial n}\right] ds_{P}$](img920.gif) . . |
(7.8) |
W zagadnieniach Dirichleta i Neumanna dla równania Laplace'a wartości
brzegowe funkcji ![]() lub jej pochodnej normalnej
lub jej pochodnej normalnej ![]() mogą być zadawane osobno lecz nie jednocześnie razem. W celu uzyskania
rozwiązania zagadnienia Dirichleta (7.1)-(7.2)
lub Neumanna (7.3)-(7.4)
należy tak przekształcić wzór (7.8), aby
wyeliminować z niego niewiadome wartości brzegowe. Można to zrobić przez
wprowadzenie pojęcia funkcji Greena.
mogą być zadawane osobno lecz nie jednocześnie razem. W celu uzyskania
rozwiązania zagadnienia Dirichleta (7.1)-(7.2)
lub Neumanna (7.3)-(7.4)
należy tak przekształcić wzór (7.8), aby
wyeliminować z niego niewiadome wartości brzegowe. Można to zrobić przez
wprowadzenie pojęcia funkcji Greena.
Załóżmy teraz, że ![]() jest pewną funkcją harmoniczną, tzn.
jest pewną funkcją harmoniczną, tzn. ![]() .
Z drugiej tożsamości Greena (6.6) otrzymujemy
.
Z drugiej tożsamości Greena (6.6) otrzymujemy
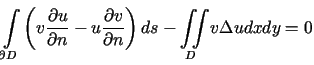 . . |
(7.9) |
Dodając stronami (7.7) i (7.9), po pogrupowaniu odpowiadających sobie wyrazów, otrzymujemy wzór
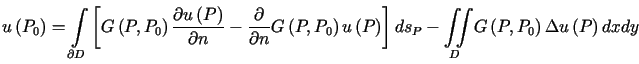 , , |
(7.10) |
gdzie
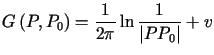 . . |
(7.11) |
Funkcja ![]() spełnia równanie
spełnia równanie ![]() w
w![]() za wyjątkiem punktu
za wyjątkiem punktu![]() .
Funkcję
.
Funkcję ![]() występującą we wzorze (7.11) wybieramy w
ten sposób, aby
występującą we wzorze (7.11) wybieramy w
ten sposób, aby
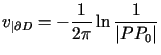 dla
dla |
(7.12) |
a to oznacza, że ![]() .
.
Funkcja ![]() dana wzorem (7.11) i spełniająca warunek
brzegowy (7.12) nazywana jest funkcją
Greena zagadnienia Dirichleta dla równania Laplace'a.
dana wzorem (7.11) i spełniająca warunek
brzegowy (7.12) nazywana jest funkcją
Greena zagadnienia Dirichleta dla równania Laplace'a.
Jeśli funkcja ta jest znana, to wzór (7.10) przedstawia rozwiązanie zagadnienia Dirichleta dla równania Laplace'a (7.1)-(7.2) w postaci
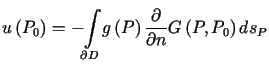 . . |
(7.13) |
Aby wyznaczyć funkcję Greena ![]() ,
należy rozwiązać szczególne zagadnienie Dirichleta z warunkiem brzegowym
(7.12). Jest ono jednak znacznie łatwiejsze
do rozwiązania niż rozważane zagadnienie wyjściowe, ponieważ w warunku
brzegowym występuje konkretna funkcja.
,
należy rozwiązać szczególne zagadnienie Dirichleta z warunkiem brzegowym
(7.12). Jest ono jednak znacznie łatwiejsze
do rozwiązania niż rozważane zagadnienie wyjściowe, ponieważ w warunku
brzegowym występuje konkretna funkcja.
Analogicznie można wyprowadzić wzór przedstawiający rozwiązanie zagadnienia Neumanna.
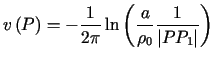 .
.Gdy ![]() ,
to z podobieństwa trójkątów
,
to z podobieństwa trójkątów![]() i
i ![]() (jeden kąt wspólny oraz
(jeden kąt wspólny oraz
![]() )
wynika, że
)
wynika, że
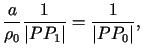
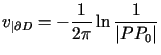 ,
,Zatem funkcja Greena zagadnienia Dirichleta dla koła dana jest wzorem
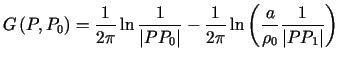 . . |
(7.14) |
Dowodzi się, że pochodna ![]() dla
dla![]() może być obliczona ze wzoru
może być obliczona ze wzoru
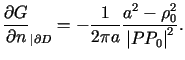
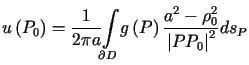 . . |
(7.15) |
Wzór (7.15) we współrzędnych biegunowych można zapisać jako
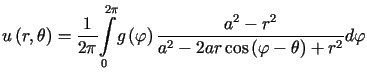 , , |
(7.16) |
gdzie współrzędne biegunowe punktu ![]() oznaczone są przez
oznaczone są przez![]() a współrzędne punktu
a współrzędne punktu ![]() na okręgu przez
na okręgu przez ![]() .
Wzór (7.16) nosi nazwę
wzoru całkowego
Poissona dla funkcji harmonicznej w kole.
.
Wzór (7.16) nosi nazwę
wzoru całkowego
Poissona dla funkcji harmonicznej w kole.