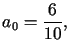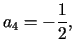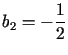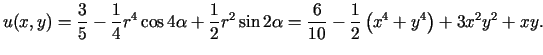Next:Metoda
odwzorowań konforemnychUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
funkcji GreenaSpis
rzeczy
Metoda szeregów Fouriera dla
koła
Rozważamy równanie Laplace'a (7.1) z funkcją
niewiadomą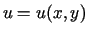
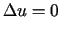 dla
dla 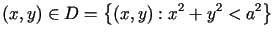 |
(7.17) |
z warunkiem brzegowym
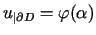 dla
dla ![$\displaystyle \alpha\in\lbrack0,2\pi]$](img957.gif) ,
, gdzie
gdzie 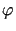 jest daną funkcją ciągłą, która może być przedstawiona w postaci sumy trygonometrycznego
szeregu Fouriera.
jest daną funkcją ciągłą, która może być przedstawiona w postaci sumy trygonometrycznego
szeregu Fouriera.
Jedna z metod rozwiązania oparta jest na przedstawieniu niewiadomej
funkcji harmonicznej 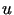 w postaci części rzeczywistej pewnej funkcji holomorficznej w kole
w postaci części rzeczywistej pewnej funkcji holomorficznej w kole 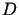
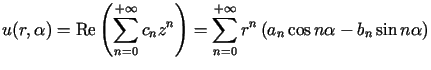 , , |
(7.18) |
gdzie
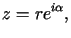
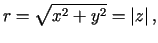
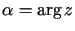 ,
, 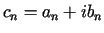 .
. Z warunku brzegowego otrzymujemy, że dla
Z warunku brzegowego otrzymujemy, że dla 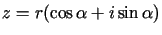 musi zachodzić równość
musi zachodzić równość
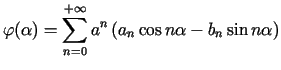 dla
dla ![$\displaystyle \alpha\in\lbrack0,2\pi].$](img965.gif) Z własności trygonometrycznych szeregów Fouriera wynika stąd, że
Z własności trygonometrycznych szeregów Fouriera wynika stąd, że
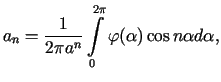 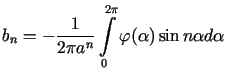 |
(7.19) |
dla 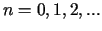
Otrzymane rozwiązanie należy ostatecznie zapisać w postaci jawnej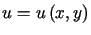 .
.
P r z y k ł a d
Rozwiązać zagadnienie Dirichleta (7.17)
dla 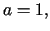
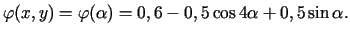
Ze wzorów (7.19) wynika, że
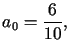
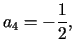
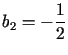 zaś pozostałe współczynniki są równe zero.
zaś pozostałe współczynniki są równe zero.
W takim razie rozwiązanie zagadnienia wyraża się wzorem
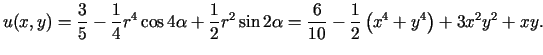 Poniższy rysunek przedstawia wykres rozwiązania
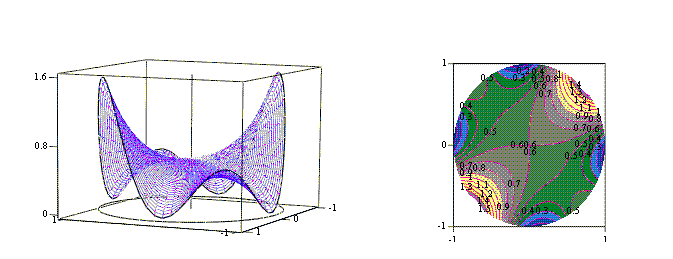
Poniższy rysunek przedstawia wykres rozwiązania 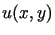 oraz jego plan warstwicowy.
oraz jego plan warstwicowy.
 Animacja przedstawia obrót rozwiązania dookoła osi pionowej.
Animacja przedstawia obrót rozwiązania dookoła osi pionowej.
Animacja w formacie avi (331
KB)
Animowany gif (134 KB)




Next:Metoda
odwzorowań konforemnychUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
funkcji GreenaSpis
rzeczy
Administrator 2003-02-19
![]() w postaci części rzeczywistej pewnej funkcji holomorficznej w kole
w postaci części rzeczywistej pewnej funkcji holomorficznej w kole ![]()
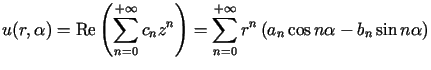 ,
,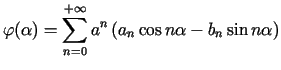 dla
dla 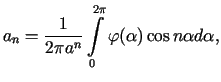
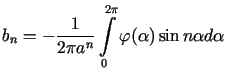
![]()
![]() .
.
![]()
![]()