



Next:Jednoznaczność
zagadnienia Dirichleta iUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
szeregów Fouriera dlaSpis
rzeczy
Metoda odwzorowań konforemnych
Rozważmy zagadnienie Dirichleta dla równania Laplace'a w półpłaszczyźnie
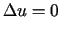 dla
dla 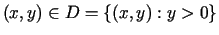 . . |
(7.20) |
Załóżmy, że szukana funkcja 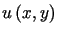 jest ciągła dla
jest ciągła dla 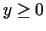 ,
ograniczona w nieskończoności i spełnia warunek brzegowy
,
ograniczona w nieskończoności i spełnia warunek brzegowy
gdzie 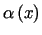 jest daną funkcją ograniczoną w nieskończoności.
jest daną funkcją ograniczoną w nieskończoności.
Z teorii funkcji zmiennych zespolonych wiadomo, że funkcja
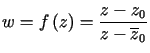 jest odwzorowaniem konforemnym półpłaszczyzny
jest odwzorowaniem konforemnym półpłaszczyzny 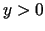 w koło jednostkowe
w koło jednostkowe 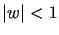 ,
przy którym brzeg półpłaszczyzny (tzn. prosta
,
przy którym brzeg półpłaszczyzny (tzn. prosta 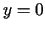 )
przechodzi na okrąg
)
przechodzi na okrąg 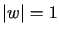 ,
a punkt
,
a punkt 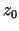 w punkt
w punkt 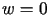 .
Wówczas funkcja
.
Wówczas funkcja 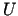 określona jako
określona jako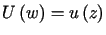 ,
gdzie
,
gdzie 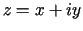 ,
jest funkcją harmoniczną w kole
,
jest funkcją harmoniczną w kole 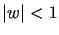 taką, że
taką, że
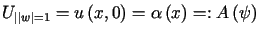 ,
, gdzie
gdzie 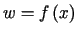 ,
, 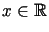 (patrz zadanie
(patrz zadanie 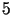 z poprzedniego wykładu).
z poprzedniego wykładu).
Z twierdzenia Gaussa o wartości średniej dla funkcji harmonicznych wynika,
że
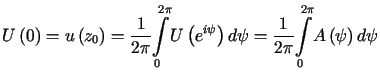 . . |
(7.22) |
Ponieważ
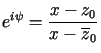 ,
więc
,
więc 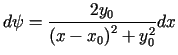 .
. Zamieniając zmienne w całce (7.22), otrzymujemy
Zamieniając zmienne w całce (7.22), otrzymujemy
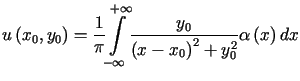 . . |
(7.23) |
Wzór (7.23) przedstawia rozwiązanie zagadnienia
(7.20)-(7.21).




Next:Jednoznaczność
zagadnienia Dirichleta iUp:Zagadnienia
brzegowe dla równańPrevious:Metoda
szeregów Fouriera dlaSpis
rzeczy
Administrator 2003-02-19
![]() jest ciągła dla
jest ciągła dla ![]() ,
ograniczona w nieskończoności i spełnia warunek brzegowy
,
ograniczona w nieskończoności i spełnia warunek brzegowy
![]() jest daną funkcją ograniczoną w nieskończoności.
jest daną funkcją ograniczoną w nieskończoności.
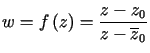
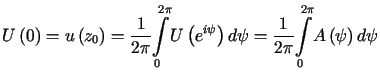 .
.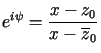 ,
więc
,
więc 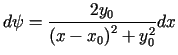 .
.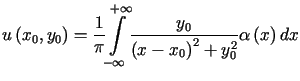 .
.