W wykładzie tym przybliżymy Wam pojęcie wymiaru, charakterystycznej cechy obiektów geometrycznych. Bardziej szczegółowo opowiemy o dziwnym wymiarze, zwanym wymiarem Minkowskiego. Policzymy ile wynosi dla różnych fraktali. Sami będziecie mogli policzyć wymiar różnych zbiorów, przy pomocy "Systemu do liczenia wymiaru Minkowskiego fraktali", który można ściągnąć z tej strony.
Co to jest wymiar?
Z punktu widzenia geometrii klasycznej wymiar figury geometrycznej równa się liczbie współrzędnych potrzebnych do określenia położenia dowolnego punktu tej figury. A więc dla odcinka, okręgu lub kostki sześciennej wymiar przyjmuje wartości całkowite.
Gdybyśmy chcieli policzyć wymiar jakiegoś fraktala powinniśmy skorzystać z innej definicji. Jak się zaraz okaże, wymiary fraktalne tych dziwnych zbiorów o skomplikowanej budowie, nie przyjmują wartości całkowitych. Na przykład dywan Sierpińskiego ma wymiar fraktalny równy 1.5849...
|
Skonstruowanie takiej definicji wymiaru, aby obejmowała przypadki geometrii klasycznej i fraktalnej było bardzo trudne i wielu matematyków z początku XX wieku zmagało się z tym problemem. Matematyka wyróżnia kilka różnych definicji wymiaru. Historia wymiaru fraktalnego sięga pracy Hausdorffa z 1918 r. Jednak definicja tego co później zostało nazwane wymiarem Hausdorffa (lub Hausdorffa-Besicovitcha) jest trudna do zastosowania w praktyce.
Jeśli mamy do czynienia z konkretnymi problemami, to często wygodniej jest skorzystać z wymiaru Minkowskiego, zwanego wymiarem pudełkowym, który jest łatwy do policzenia na komputerze. Klasycznym przykładem jest pomiar długości linii brzegowej Wielkiej Brytanii.
Sprawdźmy czy odcinek lub kwadrat mają wymiar Minkowskiego zgodny z naszą intuicją.
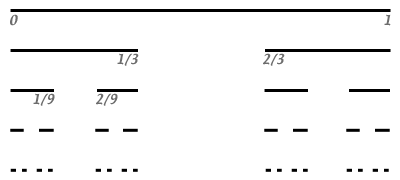
W celu obliczenia wymiaru odcinka F=[0, 1] pokrywamy go dostatecznie małymi odcinkami miarowymi e i wyznaczamy ich liczbę Ne (F ):
| e =1 | Ne (F )=1 |  |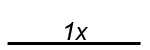
|
e =1/2 |
Ne (F )=2 |
 |
|
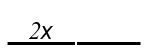e =1/4 |
Ne (F )=4 |
 |
| ... | ||
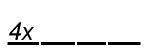| e =1/2k | Ne (F )=2k |  |
Zmniejszając długość odcinka miarowego, otrzymujemy wzrost liczby odcinków pokrywających naszą linię gładką. Zachodzi zależność Ne (F )= ~1/e .
Zgodnie z definicją wymiar Minkowskiego wynosi
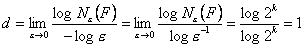
Definicja wymiaru Minkowskiego doprowadziła nas do intuicyjnej wartości wymiaru odcinka.
Analogicznie można policzyć wymiar innych figur geometrycznych.
[Wymiar kwadratu]
[Wymiar sześcianu]
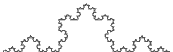
Wiemy już, że wymiar Minkowskiego zbiorów typu odcinek lub kwadrat, zgodny jest z naszą intuicyjną definicją. Teraz policzymy wymiar kilku fraktali, takich jak zbiór Cantora, krzywa Kocha (brzeg płatka śniegu), dywan Sierpińskiego, trójkąt Sierpińskiego i piramida Sierpińskiego.
Jak liczyć wymiar na komputerze? Próbując policzyć wymiar Minkowskiego na komputerze, bardzo szybko napotykamy na problemy. Na komputerze nie możemy zmniejszać e w nieskończoność, a wynik logarytmu jest podawany w zaokrągleniu. Poza tym pamiętajmy, że komputer operuje na danych dyskretnych. Nie możemy zmniejszyć e poniżej rozdzielczości (odległości pomiędzy punktami pomiarowymi), w której zapisany jest zbiór. Jeżeli byśmy tak postąpili, to zbiór traktowany byłby jako zbiór złożony ze skończonej liczby punktów. A wymiar punktu lub zbioru złożonego ze skończonej liczby punktów jest zero. Aby ominąć te niedogodności musimy się uciec do pewnego wybiegu. Pokrywamy zbiór siatką o boku e i liczymy do ilu kostek wpadają punkty mierzonego zbioru. Powtarzamy to dla kilku e. Jak pamiętamy wymiar jest zdefiniowany jako stosunek logarytmu ilości kostek do logarytmu e. Wartości zaznaczamy na wykresie logarytmicznym.
Wszystko to wygląda bardzo interesująco. Jednak zastanawiacie się zapewne do czego może służyć znajomość wymiaru Minkowskiego. Tutaj znajdziecie przykłady zastosowań.
|
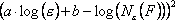, liczona dla wszystkich punktach z wykresu, była jak najmniejsza.